Research Article - (2024) Volume 13, Issue 3
This paper aims to evolve a fully automatized segmentation and detection of cerebral tumors using medical resonance images. To solve the problem of manual segmentation, which is a time consuming, error prone and delicate procedure, we implement two optically based segmentation methods based in our previous works [1-3] in the same architecture to improve the performance and accuracy. We combine the Vander Lugt optical Correlator (VLC) with a new approach based on Optical Scanning Holography (OSH). The two main characteristics of these methods are rapidity and automaticity, which makes our approach relevant, compared to other segmentation methods. The suggested method achieves high accurate detection of tumors. We have achieved a principal objective to upgrade the active contour theory from semiautomatic to automatic status by means of the OSH and VLC techniques, which leads to a more reliable brain tumor detection. In addition, it provides more reliable performances by the averages of sensitivity equals to 0.98, Hausdorff distance equals to 2.00, dice coefficient equals to 0.98, specificity equals to 1.00 and more rapidly with computation time averaging 0.30 seconds per frame. The underlying physics behind the hybrid method is the trustworthy extraction maxima of components in phase of the scanned current by OSH and the ones deduced from the correlation plane by VLC that correspond to the tumors’ positions.
Brain tumor detection • Active contour • Fully automatic segmentation • Optical Scanning Holography (OSH) • Vander Lugt optical Correlator (VLC)
Medical imaging is a precious tool for diagnosis, surgical guidance and evaluating the effectiveness of treatments. In addition, it is a potent tool that provides an instant insight into medical anomalies by providing visual images of the internal organs or tissues in the human body. Tumors in the brain are considered one of the most difficult malignancies in terms of diagnosis due to their intricate pathology [1-5]. This challenge stems from the heterogeneous nature of some pathological tissues (i.e., overlapping with healthy brain tissues). The Magnetic Resonance Imaging (MRI) has significant potential to be an alternative to existing imaging modalities on interventional procedures such as biopsies, due to its enhanced contrast with soft tissue and no ionizing radiations [6]. The detailed characteristics of brain tumors can be visualized using such imaging modalities as x-ray, ultrasound, Computed Tomography (CT) and Magnetic Resonance Imaging (MRI), allowing clinical physicians to understand the texture of cerebral tumors and thus determine the type of therapy. In terms of its position in accordance with the environment, the location and the extent of the tumor are the key factors in the therapy decision [7]. Accurate cerebral tumor detection and segmentation can assist in understanding the lesion/deficit relationship to enable prediction of clinical diagnosis and prediction of prognosis, as well as monitoring the evolution of brain pathology over time [8].
Segmentation of brain tumors is a vital task in medical image processing since early detection is critical for improving treatment options and survival rates. In one study, authors [9] used multi-atlas patch based methods with a suggested probabilistic model to automate the segmentation of brain tumors. However, these methods have limitations, such as the loss of delicate structures due to image resampling, which can negatively impact core segmentation. Li, et al., [10] proposed an alternative probabilistic model which combined a sparse representation with a random markov field to enhance both spatial and structural variability. Nevertheless, the accuracy of this model decreased slightly when dealing with low grade genuine data due to imprecise pathological features. In [11], the authors presented a hybrid method of intensity image segmentation combining a technical optical contour and two numerical algorithms to stitch edge points or image segmentation. This approach has prospective applications in both medical and biological imaging as a powerful technique for large image segmentation in real time. Another approach, the Potential Field Segmentation (PFS) algorithm, was proposed in [12], which uses the potential gravitational field analogy in physics by considering pixel intensities as masses that create a potential field. Although this algorithm calculates the summation of the individual field potentials and an adaptive potential threshold, the vast computational time was a problem, especially for large input image sizes. Recently, Banerjee, et al., [13] introduced the 3D segmentation of cerebral tumors by estimating brain tumor volume as detected by visual salience in Regions of Interest (ROI) and both small and large Volumes of Interest (VOI). Furthermore, additional studies [14-18] explore more applications for brain tumor, prostate segmentation and volumetric measures of subcortical structures in MRI.
In this work, we have developed a hybrid method to perform a faster and automatic brain tumor detection and segmentation. Our approach results from the combination of two techniques. The first one is Optical Scanning Holography (OSH) [19], which was initially suggested in 1979 by Poon and Korpel and developed by Poon [20,21]. It consists of a real time recording method, while the holographic information’s of a 3D object can be obtained with a single two dimensional optical scan. Our proposal is combining an off-axis optical scan, carried by a heterodyne fringe model, with the display of an MR image using a spatial light modulator. The digital collection of the output in-phase component enables the extraction of a highly accurate distribution of biological tissues, which facilitates the precise localization of one of the tumors based on its maximum position. Another component of the method is the vander lugt correlator, which was initially proposed in 1963 [22]. This technique involves the reliable extraction of maximum peaks in the correlation plane, which correspond to the tumor positions. The correlator is composed of three planes, namely, an input MR image plane, a filter plane and an output plane that allows for the localization of the brain tumor target. On the basis of our works [1,2] our contributions in this paper are:
• Our method needs between 0.20 s and 0.60 s to segment a brain tumor, which is one order of magnitude quicker than most of state of the art methods.
• We propose a hybrid method combining two optically based segmentation approaches of our previous works; the vander lugt VLC optical correlator and Optical Scanning Holography (OSH) to reach a very precise detection of tumor tissues.
• We have provided the display of an MRI image by a Spatial Light Modulator (SLM); the MRI image is a binary image, the SLM used can produce an off shift range close to 2π, which leads to excellent diffraction effectiveness.
This hybrid method preserves the characteristics of speed and automaticity and reduces the error rate. Therefore, short computation time (in few seconds) and high segmentation accuracy performance.
Experimental setup
Figure 1 illustrates the schematic of a combination of techniques to realize an accurate detection and segmentation of brains' tumors [1-3]. Alaser beam of frequency ω0 is separated by a Polarizing Beam Splitter (PBS) placed between the OSH and VLC. In an OSH architecture, the laser beam of frequency ω0 is shifted upward by frequencies Ω and Ω+ΔΩ into two beams with acoustic optic modulators AOM1 and AOM2, respectively. The emerging beams of the AOM are subsequently collimated by collimators BE2 and BE3. The beam exiting BE3 is then considered as a plane wave at frequency ω0+Ω+ΔΩ being projected onto the object through the x-y scanner, while the L1 lens produces a spherical wave at frequency ω0+Ω being projected onto the object, T(x,y,z). The two rays are recombined by the Beam Splitter (BS) and projected toward the object T(x,y,z) into the lens L2. The object is positioned at a distance z away from the back focal plane of the lens. The x-y scanner is used to scan the MRI of the brain tumor uniformly, row by row. Thus, each scanned row of the object will result in a line of the hologram at the same vertical position. The PD1 and PD2 photodetectors along each scan row are used to capture the optical signal scattered by the object and the heterodyne frequency information ΔΩ to be used as the reference signal, respectively, then to be converted into electrical signals by the lock in amplifier. The In-phase and the Quadrature (Q)-phase outputs of the lock in amplifier give a sine hologram and cosine hologram. Thus, a precise distribution of the tissue is obtained by using this in phase tool. The obtained maximum identifies perfectly the position of the tumor.
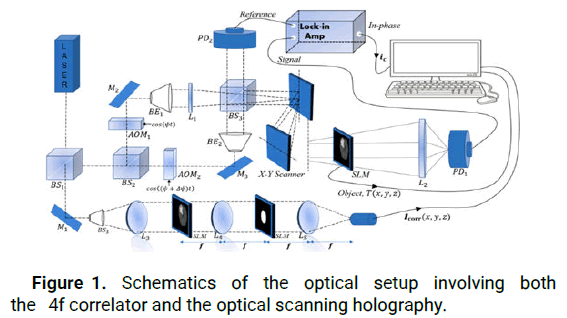
Figure 1: Schematics of the optical setup involving both the 4f correlator and the optical scanning holography.
On the other hand, The architecture called 4f or double diffraction and under specific conditions, called Vander Lugt assembly, is an optical correlator where it is first to realize the product of Fourier transforms of two images before applying a new Fourier transform on the result. This architecture uses a filter whose transmission in amplitude is proportional to the complex conjugate of the Fourier transform of the reference object.
The main idea of the principle of optical correlation is to find the appropriate filter so that in the correlation image appears a peak, called correlation peak, whose position of the maximum corresponds to the position of the object of interest in the scene image. The lens L3 serves to collimate the beam to obtain a wave plane at the system's entrance. The correlator used for detecting brain tumors includes three planes: An input image plane projected in SLM1, a filter plane projected in SLM2 and an output plane that localizes the target. The correlation plane which accurately detects the position of the brain tumor and the appropriate filter size for the tumor size can be determined by identifying the maximum value of all peaks in the output planes.
Detection phase
Optical Scanning Holography (OSH): Optical Scanning Holography (OSH) is a method of holographic recording with a singular pixel. Pioneered by Poon, [19] and the original idea of OSH was dated back to the late 70’s when Poon and Korpel, investigated bipolar incoherent image processing with their two pupil acousto optic heterodyne scanning image processing system [23-25]. OSH is a specialized two pupil heterodyne image processing system and it can extract holographic information of a 3D object using a single raster optical scan. The OSH offers the ability to produce a highresolution hologram due to the properties of scanning holograms. However, it is necessary to notice that the (OSH) presents some weaknesses which it is essential to detect and thus to solve. Firstly, OSH based on 2D scanning generally relies on mechanical scanning, which affects the quality of the recorded hologram because of the inevitable vibration of the mechanical system.
The optical scanning holography involves both active optical scanning and optical heterodyning. An optical scanner or optical processor scans an object with an optical beam by displacing the beam. A photodetector takes all the incoming light and provides an electrical output that can be stored or displayed. The optical information will therefore have been converted into electrical information. However, a simple optical scanning system that uses direct optical detection cannot extract the phase information from the incoming complex field. Since holography involves the preservation of phase information, we are faced with the task of finding a method to preserve the phase information during the photo detection of an optical scan in order to record the holographic information. The key to this problem is optical heterodyning. The complex combined optical scanning field, E(x,y,z), situated at a distance z from the focal plane of the two lenses, is given by the following equation:
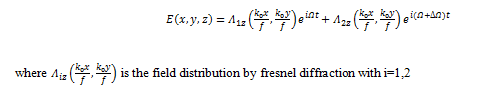
The photodetector, which is affected by the incident intensity of the transmitted optical field, produces a current given by:
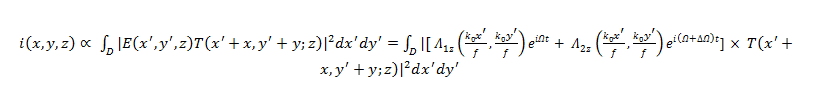
Across a Bandpass Filter (BPF) set to a frequency of Ω, the heterodyne current becomes:
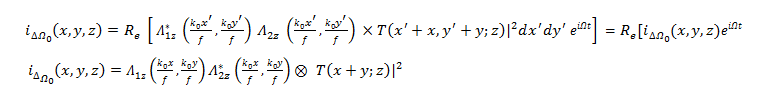
Which represents the output current holding the amplitude and phase information of the heterodyne current? The current amplitude and phase information is the scanned version of the object |T|2. In this case, the Optical Transfer Function (OTF) of the system can be defined as follows:
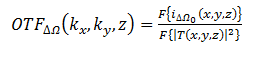
This gives us the following equations:
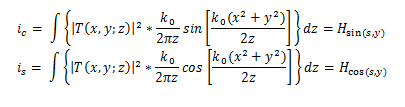
The methodology put forth in this study centers on two distinct currents, namely the in-phase component ic(x,y) and the quadrature component is(x,y), which are both extracted from the heterodyne current of the MR scanned image. The primary objective of this approach is to identify abnormal tissue by detecting the highest peak of the in-phase components shown in the MR scan, which is based on the fundamental principle of this methodology.
Vander Lugt Correlator (VLC)
Optical correlators estimate a reference object's position in a scene containing a structured background and noise. Besides, they proved to be a fast tool that responds to this need due to their massive parallelism allowing obtaining the correlation of two images in a few nanoseconds. The 4f optical correlator is based on a double Fourier transformation shown in Figure 1.
In the frequency plane, the mathematical model of the optical correlation principle is the product of the fourier transforms of the two images S(u,v) and H*(u,v).
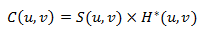
With H(u,v) in the frequency plane, is written:
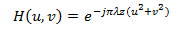
The main idea of the principle of optical correlation consists of finding a matched filter H*(u,v), so that in the correlation image c(x,y) appears a peak, called the correlation peak, whose maximum position corresponds to the object of interest in the scene image. Optical systems, especially the coherent correlator known as 4f or derived correlators, represent robust optical recognition architecture because of their capacity for parallel processing. The diffraction theory shows that incoherent light, the Fourier transform of an image in front of the lens, is found at its focal point. This section establishes that the Fourier transform (the kernel of the correlation) is natural in optics through a lens.
The Fresnel diffraction integral leads to the Fresnel propagation equation, which takes the following form in the frequency domain:
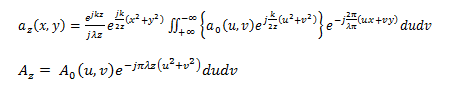

Finally, we obtain the correlation intensity recorded by this quadratic detector from the squared modulus of this Fourier transform:
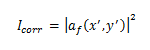
Hence, we extract the highest values of all output peaks that correctly define the positions of brain tumors. In addition, due to the size of tumors in MR images, we propose a specific elliptical shaped filter that is able to detect tumor centers and accommodate all tumor sizes (Figure 2).
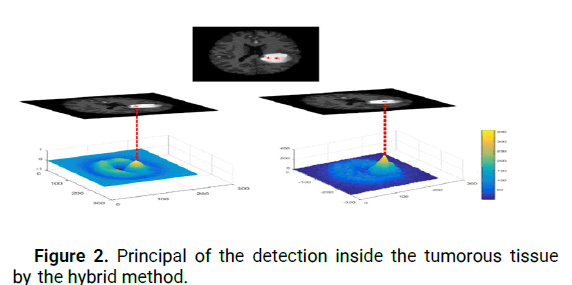
Figure 2: Principal of the detection inside the tumorous tissue by the hybrid method.
Segmentation phase: Manual segmentation of the brain tumors concerning cancer diagnosis of a considerable amount of MRI images produced in the clinical system is a time consuming and challenging task. There is a necessity for automated brain tumor segmentation [26]. Brain tumor segmentation involves separating the various tumor tissues (tumor, edema and necrosis) from benign brain tissues: GM, WM and CSF [27]. There are several brain MR image segmentation applications in neurology, such as, operational planning, quantitative analysis and functional imaging [28]. Quick and accurate diagnosis helps shorten intraoperative waiting time and makes a correct plan for the brain tumor resection [4]. In addition, many patients are increasingly affected by brain tumors. Thus, manual tumor determination is becoming a less recommendable approach. For this reason, the number of publications on automatic brain tumor segmentation has increased exponentially in recent years.
The active contour model, a recent approach that has made significant progress in many applications, presents a better segmentation technique compared to those described previously. It delivers better robustness and resistance to noise. The main problem with this technique lies in the fact that it is based on the definition of a starting contour of the object to be detected (what is called the initial contour), which is indispensable for the segmentation sequences. This step is performed manually, which requires a user to target the region of interest which gives this method a semi-automatic property. The "active contours" start with an input contour and dynamically change its shape until it reaches the desired boundary, reducing the energy at each iteration until convergence is reached. It is obtained when a balance exists between the "external" energies which attract the contour to its location and the "internal" energies which keep it smooth.
This hybrid method aims to remedy these intrinsic limitations of the problem mentioned above of active contour as best as possible. This step increased the accuracy of the proposed system in terms of brain tumor detection. Indeed, the proposed method has demonstrated high accuracy as required in brain tumor segmentation in clinical imaging applications. Hence, this is a powerful technique to detect tumor tissue in magnetic resonance images, when compared to one of the newly published methods [29-31], the suggested method outperforms its accuracy and computing time. Consequently, we have achieved a principal objective to move the image segmentation from semiautomatic to automatic status. The hybrid method detects tumor tissue and facilitates the energy calculation of active contours. Using the initially detected contour Ci, we compute the MR image averages I(x; y) both inside and outside Ci to constrain the active contour model:
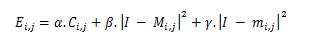
Where: α=β=γ=1 is defined as fixed values Ci,j is the starting contour identified by the hybrid method
mi,j is the average of the input MR image I(x,y) within the initial contour Ci,j
Mi,j is the average of the entry MR image I(x,y) over the starting contour Ci,j
Besides, the variation of the initial contour found by the proposed architecture is realized by the scheduling of the proposed active contour model using the finite differences obtained after linearization and discretization of the equation energy (12). Figure 3 illustrates examples of hybrid tumor segmentation.
The overall algorithm of the simulated method is presented in program 1. The input image and the predefined filter are denoted by I (x,y) and r (x,y), respectively, where F and F-1 denote the Fourier transform and the inverse Fourier transform, respectively. Conj denotes the conjugate operator used for the correlation, otherwise the correlation will be a convolution. Program simulated optical correlation framework for segmentation of the region of interest.

Within this section, we begin by evaluating the performance of the proposed method in detecting brain tumors, using four parameters: The center of the tumor (C1), the maximum peak of the in-phase component (L1) obtained by the OSH technique and the center of the tumor (C2) and the maximum peak in the correlation plane (L2) obtained by the VLC technique. These tests were conducted on two datasets, BRATS 2012 and BRATS 2013, both of which have ground truth data available [32,33].
To differentiate between healthy and affected brains, we studied the parameter L for MRIs using the OSH and VLC techniques. Figure 4 illustrates the distribution of L in the three models. We observed that L values in healthy brains ranged from 10 to 60, whereas in brain tumor images, the maximum peak in the correlation plane obtained by VLC was between 250 and 300. Similarly, the maximum peak of the in-phase component obtained by OSH was between 300 and 350. The accuracy of the cerebral tumor location is mainly based on Ci, which is determined by the hybrid method, by measuring how accurately Ci is detected within the tumor. The advantage of this method is that it provides two highly accurate detections of the tumor on the same MR image, which improves accuracy over other reported methods. Figure 2 illustrates the principle of detecting the tumor within the tumorous tissue using the hybrid method (the VLC and OSH techniques). For the purpose of brain tumor segmentation, the hybrid method is assessed using four similarity metrics: Sensitivity sen, Dice coefficient (D), Hausdorff Distance (Hd) and Specificity (Spe). These metrics are calculated as follows:
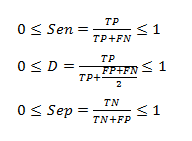
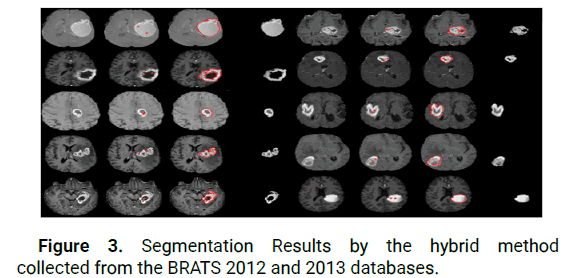
Figure 3: Segmentation Results by the hybrid method collected from the BRATS 2012 and 2013 databases.
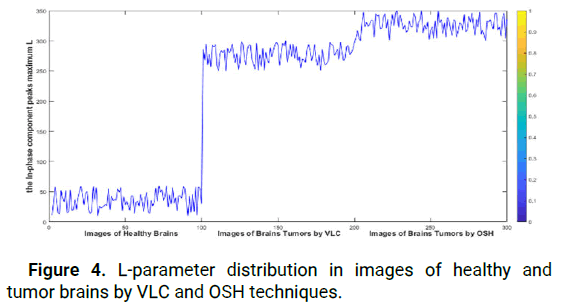
Figure 4: L-parameter distribution in images of healthy and tumor brains by VLC and OSH techniques.
The following formula is used to calculate the Sensitivity Sen (s), Dice coefficient (D), Hausdorff Distance (Hd) and Specificity (Spe) metrics. Here, TP represents true positive (pixels correctly identified as tumor tissue), TN represents true negative (pixels correctly classified as healthy tissue), FP represents false positive (healthy tissue incorrectly labeled as tumor region) and FN represents false negative (unidentified tumor tissue).
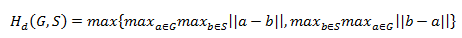
Where G is the ground truth and S is the automatically obtained result. Ideal similarity is achieved when the parameters Sen, D and Spe are equal to 1 and the absolute value of Hd(G,S) is equal to 0 (Figures 5 and 6).
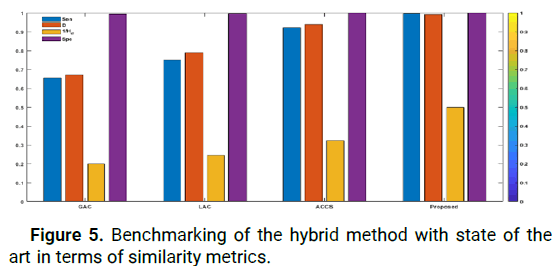
Figure 5: Benchmarking of the hybrid method with state of the art in terms of similarity metrics.
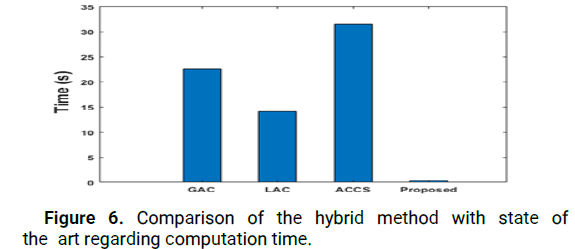
Figure 6: Comparison of the hybrid method with state of the art regarding computation time.
Following the fast automatic detection of tumor tissue using the hybrid approach, the advantages provided by the approach proposed for segmentation have been discussed in this section. To that end, various models of Active Contours (ACMs) using the hybrid approach were evaluated. To guarantee a meaningful description, all ACMs were initialized with the starting contours obtained by the hybrid technique. To evaluate the performance of the proposed method under challenging conditions related to medical imaging applications, thirty (30) patient images with various challenging segmentation conditions were used. These images included tumors of different forms, sizes and contrasts. Figure 5 compares the baseline performance of the proposed hybrid method with the Geodesic Active Contour model (GAC) [34], Localized Active Contour (LAC) [35] and cuckoo search driven Active Contours (ACCS) [36] on these 30 images. The results show that the newly proposed method outperforms other ACMs in terms of Sen, D, Hd and Spe parameters. For example, our proposed method achieved an average sensitivity value of 0.9800, which is the highest obtained, while its Hausdorff distance of 2.0000 is the lowest. Additionally, its average specificity value Spe=1.0000 shows that it can precisely classify healthy tissue and is more reliable than other MCA based approaches. It is worth mentioning that all methods achieved a high level in terms of the Spe parameter, because all original contours detected by the offered approach were located inside the tumor. As these methods evolved, the optimal segmentation contours remained within the tumor tissue, which made the FP parameter close to 0.
Furthermore, as illustrated in Figure 6, our method achieves a reduction in computation time compared to existing methods (expressed in seconds). The hybrid method is faster compared to our previous approach because it recognizes the initial tumor contour in real time, which reduces the computational time required to evolve the active contour.
This paper presents a fast and automatic brain tumor segmentation system combining two approaches of our previous works [1-3]. The first is the Vander Lugt optical Correlator (VLC) and the second is the Optical Scanning Holography (OSH). The underlying physics behind the reliable detection of brain tumor position is the extraction of the in-phase component peaks' maxima by OSH and the maximum peak in the correlation plane by VLC that correspond to the tumor position. This combination of methods retains the rapidity and automaticity characteristics and error rate reduction. Several active contour models were taken into consideration during the segmentation stage and their performances were analyzed using various similarity metrics. The results obtained from the BraTS databases of 2012 and 2013 indicate that the detection and segmentation of brain tumors have been enhanced successfully compared to the existing state of the art methods.
To Raphael Meier of the institute for medical image analysis for surgical technology and biomechanics in Switzerland at the university of Bern, who facilitated access to the multimodal comparative Brain Tumor Segmentation Study (BRATSS), the authors are grateful.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
Citation: El-Ouarzadi A, et al. "Brain Tumor Detection and Segmentation Using a Hybrid Optical Method by Active Contour". J Biol Today s World, 2024, 13(3), 1-6.
Received: 16-Dec-2023, Manuscript No. JBTW-23-120858; Editor assigned: 20-Dec-2023, Pre QC No. JBTW-23-120858 (PQ); Reviewed: 03-Jan-2024, QC No. JBTW-23-120858; Revised: 01-Jun-2024, Manuscript No. JBTW-23-120858 (R); Published: 28-Jun-2024, DOI: 10.35248/2322-3308-13.3.003
Copyright: ©2024 El-Ouarzadi A, et al. This is an openaccess article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.