Journal of Biology and Today's World

Mathematical Model of Rate of Blood Flow and Diffusion due to External and Internal Solution

Dhanorkar Gajanan^1*, Sachin Bedre² and Jadhav Keshav^{3 *}Correspondence: Dhanorkar Gajanan, Rayat Shikshan Sanstha’s Karmaveer Bhaurao Patil College Vashi, Mumbai University, Mumbai, India, Email:

Author info »

Introduction

To find stable solution of estimate the drug concentration at different sites and within the blood. When the drug is administered orally or by injected into the body, it dissolves in the blood and releases the medications into the gastrointestinal tract. The flow of drugs within the body is modulated by treating the different parts of the body as compartments and then tracking the medication as it enters and leaves each compartment. The drug leaves one compartment and enters into another one at the rate proportional to the concentration of drug present in the first compartment. It starts the medications diffuse blood cells to tissue cells and vice versa. The constant of proportionality is mainly determined by the drug, the compartment and general health of the individual (Figures 1-6).

If c(t) denotes the concentration of drug in the compartment at time t, then the rate of change of c(t) is:

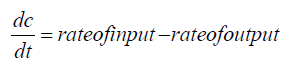
Main Result

Basic Solution of linear differential equation with mathematical model

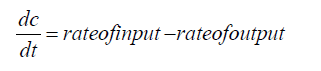
Can be found by applying particular solution method, In order to formulate a mathematical model for the blood flow due to drug absorption, we have considered two different models Model-I and Model-II.

Model-I

In this model, only two compartments viz. blood and tissue were identified as the main exchangers. The first one is the blood stream into which the drug is injected and the second one is the tissue where the drug has the therapeutic effect. We assume that blood takes a part of drug at the rate of K_b onto tissue, from tissue compartment to the venous blood with the rate of K_t and K_e is clearance rate (eliminated from blood). Let C(t) and C_t(t) denote the concentration of drug in the compartments of blood and tissue respectively and C₀ be the initial concentration of drug injected through intravenous route the body [1]. Then the mathematical form of two compartment model describing the drug administration is as shown in Figure 1.

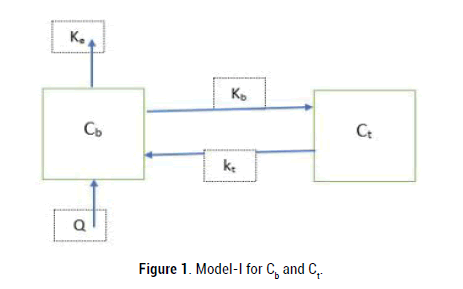
Figure 1: Model-I for C_b and C_t.

Thus the mathematical formulation in this case is governed by the system of ODEs, each equation describing the rate of change of drug concentration with respect to time in their respective compartments as [2].

Equilibrium Analysis

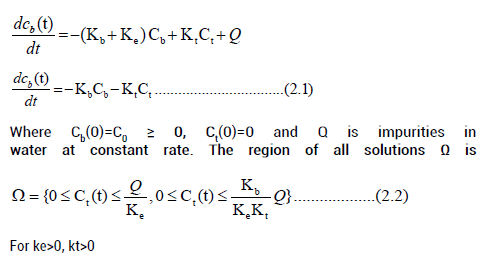
This model (2.1) has the following two nonnegative equilibrium in Ω as

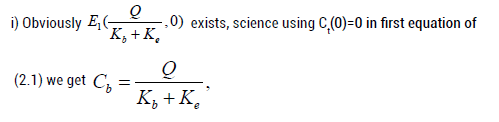
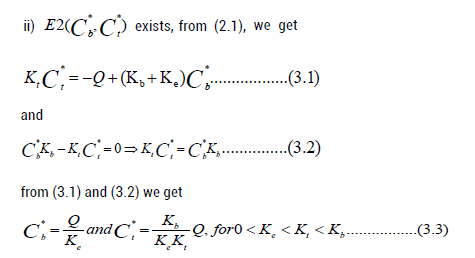
by using simulink in MATLAB and plotted the graphs for variation of drug concentration with respect to time [3,4]. Equilibrium point for particular time with respective to particular values Time t=5.1766, C_b=C_t=39.1236. Clearly we get observation in Figures 2 and 3.

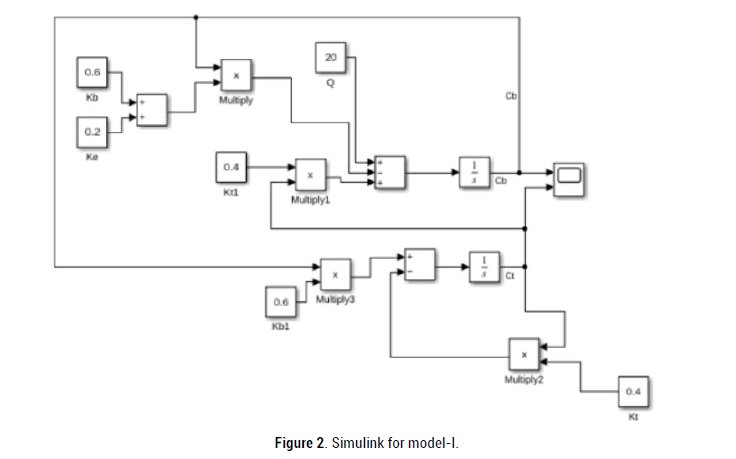
Figure 2: Simulink for model-I.

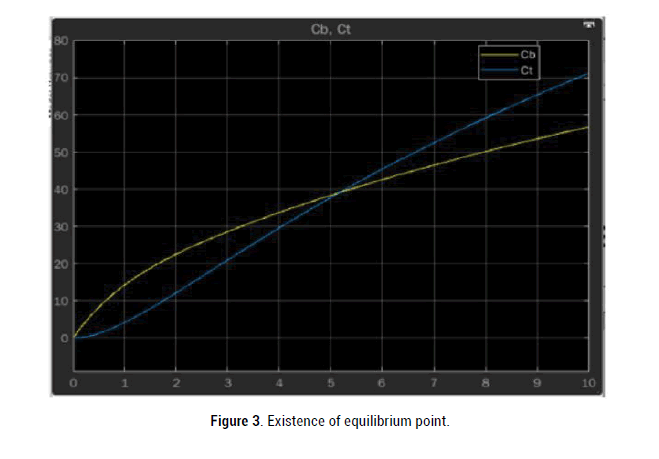
Figure 3: Existence of equilibrium point.

1) For C_b = 0 ⇒ C_t = 0

2) For K_b ⇒ ∞ ⇒ C_t ⇒ ∞

3) For K_e ⇒ 0 ⇒ C_b ⇒ 0

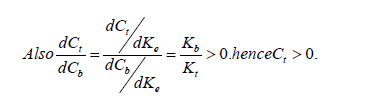
Therefore equations from (3.1) intersect in interior of the positive quadrant, hence this Model-I has non-negative equilibrium ( C_b^*,C_t^* ).

Stability Analysis

The stability of the given system (2.1) around each of the equilibrium is obtained by computing the vibrational matrix J corresponding to each equilibrium point. The Jacobian matrix corresponding to the system (2.2) is given below,

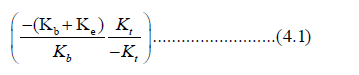
Stability depends on the Eigen values of the matrix (3.2) with characteristic equation gives solution.

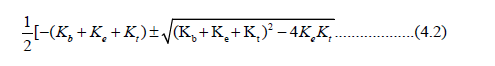
In both cases eigen values are negative showing stability of the system. Theorem 4.1. The equilibrium E(C_b^*,C_t^*) is stable.

Model-II

Assume that the consumption of drug by arterial blood towards tissue flows at the rate of K_b and from tissue compartment to the venous blood with the rate of K_t. Let K_e be the clearance rate of drug from the blood [4-6].

Let C_ab (t), C_t (t) and C_vb(t) denote the concentration of drug in the arterial blood, tissue and venous blood compartment respectively with C₀ as initial drug dosage [7,8]. Graph of the model is Figure 4.

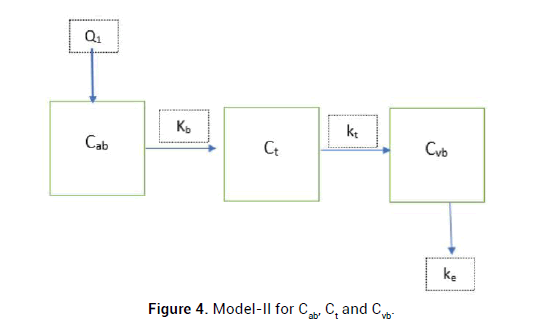
Figure 4: Model-II for C_ab, C_t and C_vb.

The mathematical model for the drug concentration with respect to these compartments with initial conditions

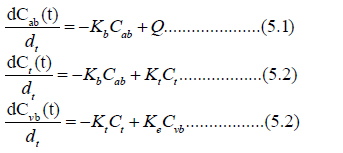
with C_ab(0)=C₀, C_t(0)=0, C_vb(0)=0 and Q is impurity in water at constant rate from arteries and venous. The region of all solutions Ω is

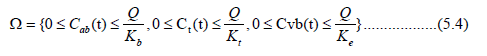
For K_e<K_t<K_b

Equilibrium Analysis

This model (5.1) has the following two nonnegative equilibrium in Ω as

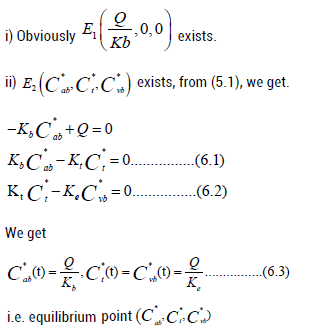
By using simulink in matlab Figures 5 and 6.

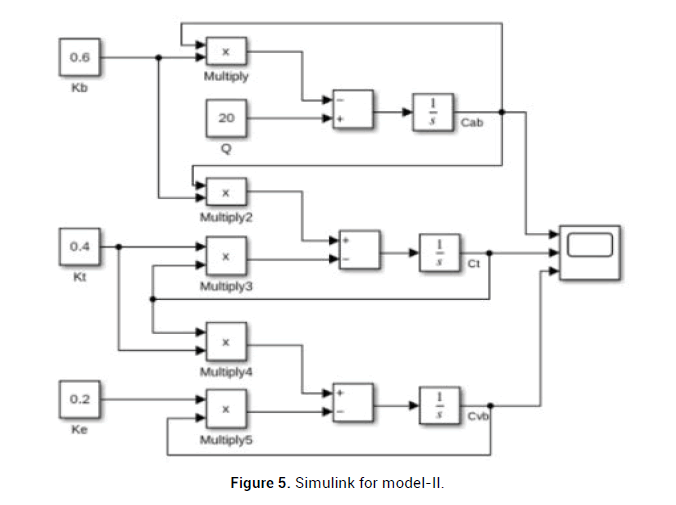
Figure 5: Simulink for model-II.

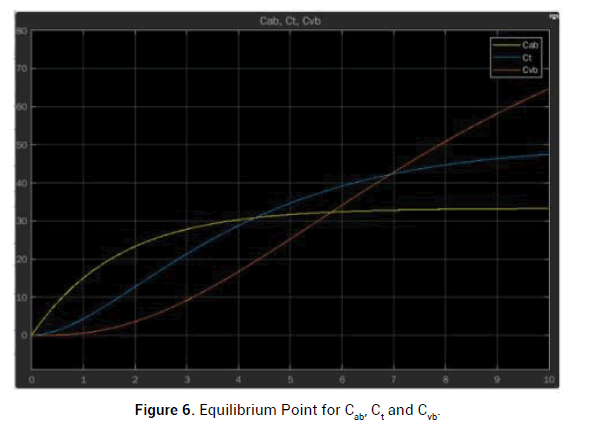
Figure 6: Equilibrium Point for C_ab, C_t and C_vb.

We get equilibrium Points for perticular points

(1) C_ab and C_t: Time: t=4.3199, C_ab= C_t=30.8333

(2) C_ab and C_vb: Time: t=5.7940, C_ab= C_t=32.3026

(3) C_vb and C_t: Time: t=6.9311, C_vb=C_t=432.1826

Conclusions

It is observed:

1) For Model-I, it is clear that concentration of drug decreases with respect to the absorption of drug in all compartment. Also from Figures we get existence of equilibrium point of concentration.

2) From Model-II, it is clear that concentration of drug decreases with respect to the absorption of drug in all compartment. The drug concentration goes on changing patient to patient depend on the condition of patient then also rate of absorption goes to stability.

From formulation of Model-I and II both are working models and applicable for the pharmaceutical and medical field for understanding diffusion of blood flow due to drug concentration.

Acknowledgement

The authors wish to thanks RUSA for providing financial support under RUSA MRP Sanction letter No: 629 2020-2021.

References

1. Khanday MA, et al. “Mathematical models for drug diffusion through the compartments of blood and tissue medium.” Alexandria J Med 53.3(2017):245-249.

   [Crossref] [Google scholar]

2. Khanday, MA & Rafiq A. “Variational finite element method to study the absorption rate of drug at various compartments through transdermal drug delivery system.” Alexandria J Med 51.3(2015):219-223.

   [Crossref] [Google scholar]

3. Misra, AK & Singh AK. “A mathematical model for unemployment.” Nonlinear Anal Real World Appl 12.1(2011)128-136.

   [Crossref] [Google scholar]

4. Misraa, AK, et al. ‘’Mathematical modeling and analysis of the depletion of dissolved oxygen in water bodies.’’ Nonlinear Anal Real World Appl 7(2006):980-996.

   [Crossref] [Google scholar]

5. Khanday, MA & Najar, A. ‘’Mathematical model for the transport of oxygen in the living tissues through capillary bed.’’ J Mech Med Bio 2015;15(4):1550055.

   [Crossref] [Google scholar]

6. Borrelli RL, Coleman CS. ‘’Differential equations, a modelling perspective.’’ John Wiley and Sons Inc 2004.
7. Dubey, B, et al. ‘’A model for fishery resource with reserve area.’’ Nonlinear Anal RealWorld Prob 4 (2003) 625–637.

   [Crossref] [Google scholar]

8. Freedman, HI & So, JWH. ‘’Global stability and persistence of simple food chains.’’ Math Biosci 76(1985):69-86.

   [Crossref] [Google scholar]