Research Article - (2017) Volume 3, Issue 2
Herein it has been made an attempt to find a theoretical explanation and build some mathematical models of the main psychophysics law derivation on the basis of an optimization principle with regards to the multi-optional situation of the process of the relation formation between external stimuli and their corresponding internal perception functions. The psychological uncertainty of such multi-optional situation is evaluated with the optional hybrid stimuli functions entropy connected within the postulated objective functional with the related perception functions. Applying the optional hybrid stimuli functions entropy conditional optimization principle we get optimal distributions of the optional hybrid stimuli functions. The proposed concept allows finding the optimal distribution of the optional hybrid stimuli functions which in its turn delivers maximal value to the objective functional and at the same time ensures satisfying the main psychophysics law conditions. The discussed approach has the significance of the scientific substantiation for the well-known Weber-Fechner law logarithmic operation with stimuli in regards to obtaining their perceptions. The performed corresponding modeling is illustrated with the necessary diagrams.
Keywords: Main law of psychophysics, Multi-optionallity, Uncertainty, Optional hybrid stimuli functions, Optional hybrid stimuli functions entropy conditional optimization principle, Optimization, Weber-Fechner law logarithmic operation, Stimulus, Perception, Psychology
In the presented research author’s opinion, formed under the related literature survey, it has been for almost a few centuries that scientists and scholars all over the globe try finding some provable explanations to human being behavioural phenomena based upon mathematically derived psychological relations and dependencies [1,2].
Corresponding assumptions are usually postulated to build a more or less justified model of the considered process [2,3]. Sometimes certain attempts towards generalizations are made and these attempts periodically look very progressive, perspective, and promising [1-4].
Closest to the presented theoretical research are the ones reflected in works [5-7]. However, in the core point [5,6] is the described there Luce’s basic axiom for the probability of a choice; and Kasianov [7], the cornerstone is the introduced by professor Kasianov [7] and widely used, although also postulated, Subjective Entropy Maximum Principle (SEMP), which nevertheless allows obtaining the identical to [5,6] mathematical view expressions, but there, one of the canonical distributions of subjective individuals’ preferences of achievable alternatives; and that in its turn means a provable structure of a theorem instead of the axiom mentioned in [5,6].
One of the latest articles Ziqian [3] proves that the process of that kind of search will apparently never end. Entropy principle by Jaynes [8,9] followed by SEMP [7] were put down into the foundation of this work. In the presented consideration the author combines the described approaches being crystallizing an alternative method for the Main Psychophysics Law (Weber-Fechner Law) [10,11] derivation on the multi-optional basis. It implies applying the hybrid optional functions entropy in order to take into account the existing diversity and broad variety in the available options with the required assessment of the options degree of uncertainty, likewise in works [12-22].
Application of entropy paradigm, likewise in works by Jaynes [8,9] and its SEMP evolution in Subjective Analysis [7] with its further development in the view of the Euler-Lagrange variational principle modification [23], gives a researcher a possibility to derive so desired explainable dependencies.
The main law of psychophysics (Weber-Fechner law) [4], pp. 128- 132, § 3.3.3, esp. P. 131, can also be derived on the basis of a certain entropy conditional optimization principle (similar with SEMP [7,10-23]).
Traditional methods of the weber-fechner law derivation
One of the possible derivations is a traditional derivation of the Weber-Fechner law that can be traced in accordance with (4, pp. 128- 132, § 3.3.3). The main suppositions are that the ratios, (4, P. 131),
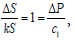(1)
where S – value of a stimulus; k – constant coefficient of the difference ΔS and stimulus ΔP values proportionality; ΔP – increment of a perception P related with the stimulus of S ; c1– constant of the increment of perception ΔP .
The expressions of (1) follow and are obtained from the accepted interrelationships, (4, P. 131):
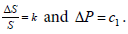(2)
Equations (2) are believed to be fulfilled in the entire diapasons of stimuli S and perceptions P values possible changes.
The acceptance of relationships (1) and (2) lead to differential equation, (4, P. 131):
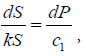(3)
with further integration, (4, P. 131):
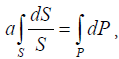(4)
where 
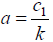(5)
Then general solution of Eq. (4), (4, P. 131):
(6)
Having 
(7)
we get from Eq. (6)
(8)
Finally, substituting (8) for its value into (6) we have the Weber- Fechner law, (4, P. 131):
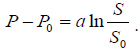(9)
The traditional derivation of the Weber-Fechner law given in Eq. (1)-(9) is conducted on the basis of suppositions (1) and (2) which are differential principles.
Hybrid optional stimuli functions entropy method of the weber-fechner law derivation
Now we propose considering an alternative to Equations 1 to 9 method of the Weber-Fechner law derivation. It will be based upon stimuli magnitude diversity and suppositions relating to this, thus the principles of the stimuli optional optimality perception with respect to the stimuli uncertainty, rather than the differential principles expressed with Equation (1) and (2).
Let us try to treat the possible relations between external stimuli and our responses to them in the view of our perceptions like objects with a multi-optional background. It is reasonably naturally to presuppose that our subconsciousness processes external stimuli unknowing the resulting perceptions, but in an optimal way, being taken into account the stimuli uncertainty.
The degree of the stimuli uncertainty is logically to be estimated with the stimuli entropy:
(10)
Here, in formula (10) N – number of stimuli values Si (the number of options being taken into consideration); the stimuli values of S are hybrid optional stimuli functions (principally these are simply their numerical magnitudes allowing logarithmic mathematical operation).
Applying proposed approach, which follows the Jaynes principle [8,9] as well as SEMP [7] as a kind of a mathematical wrapping (just a formal view envelope) with the specifically introduced notions of the stimuli optional optimality perception and the stimuli values degree of uncertainty, however not combining all that with the normalized hybrid stimuli functions into an objective functional, we get the assessment needed optimization.
In partial case of some two options being considered, which means N = 2 , it yields the purpose functional in the view of formula 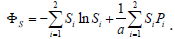(11):
(11)
In expression (11) there is no the last member likewise of the analogous functionals used in publications [7-23], the normalizing condition for the hybrid optional stimuli functions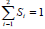 
taken into consideration with the normalizing function γ (coefficient / Lagrange uncertain multiplier / weight coefficient).
On condition of functional (11) extremum existence with respect to the hybrid optional stimuli functions:
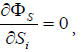(12)
and taking into account
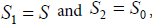(13)
and correspondingly
(14)
we obtain
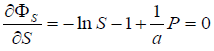(15)
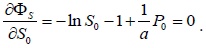(16)
The yielded result expressed with the formulae of (15) and (16) allows following the approach proposed in works [10,11]. From Equation (15) and (16), [10]:
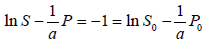(17)
(18)
Then resolving Equation (17) or (18) for P we have
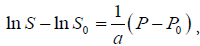(19)
and finally, [11]:
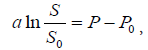(20)
the Weber-Fechner law, but now revealed on the multi-optional hybrid functions entropy conditional optimization basis.
Conditional optimal distribution of the hybrid optional stimuli functions with taking into account their entropy and normalizing condition
From functional similar to (11), but now with the normalizing condition:
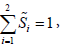(21)
for the now new normalized hybrid optional stimuli functions 
, likewise in researches [7-23]:
(22)
Where,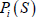 
– perception functions obtained from Equation (9) or (20), γ – normalizing function (coefficient / Lagrange uncertain multiplier / weight coefficient), and extremum existence conditions similar to (12) developed into Equations (15) and (16) or (17)
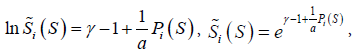(23)
applying the normalizing condition as well, it is obtainable
(24)
Then, using the result of Eq. (24) and substituting it for its value into Eq. (23)
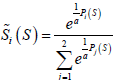(25)
Expressions of the equations of system (25) give optimal distribution of the hybrid optional stimuli functions for the objective functional (22).
From functional similar to (11), but now with the normalizing condition:
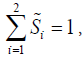(26)
for the now new normalized hybrid optional stimuli functions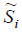 
likewise in researches [7-23]:
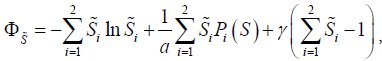(27)
Where Pi (S) – perception functions obtained from Equation (9) or (20), γ – normalizing function (coefficient / Lagrange uncertain multiplier / weight coefficient), and extremum existence conditions similar to (12) developed into Equation (15) and (16) or (17)
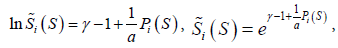(28)
applying the normalizing condition as well, it is obtainable
(29)
Then, using the result of Equation (24) and substituting it for its value into Equation (23)
(30)
Expressions of the equations of system (25) give optimal distribution of the hybrid optional stimuli functions for the objective functional (22).
The results of the mathematical models computer simulations for the presented methods Equations (1)-(25) are illustrated in Figures 1-3.
Figure 1: Perceptions as functions of the stimulus’ independent variable.
Figure 2: Optimal distribution of optional hybrid stimuli functions.
Figure 3: Entropy measure for the uncertainty of the optimal distribution of the optional hybrid stimuli functions.
The data for the conducted calculations experiments are as follows:
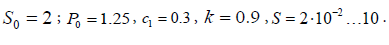(31)
Diagrams of perceptions in Figure 1 are plotted with the use of the data values (26) and following formulae:
P(S) – with the help of either equation (9) or (20) since they are identical, that is
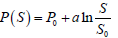
P(S0) – constant value of equations (9) or (20) when their arguments are S0 = 2 , i.e., it turns to be the initial condition expressed with the accepted equation (7):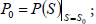 
-perception found from the optimal distribution of the optional hybrid stimuli functions (25), being inserted by their substitution for the corresponding stimuli into the previously obtained equations (9) or (20):
(32)
Graphs of the optimal distribution of the hybrid optional stimuli functions (25) are represented in Figure 2.
There, in Figure 2,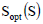 
is the curve plotted for the optimal hybrid optional stimulus function 
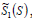Equation (25), supposedly related in an optimal way with perception (9) or (20) through functional (22): 
– the same is to function 
Equation (25), correspondingly.
The curve of the entropy measure: 
, in the view of formula (10), for the uncertainty of the optimal distribution of the optional hybrid stimuli functions Equation (25) is illustrated in Figure 3.
Also, in Figure 3, it is shown the maximal value of the entropy for the considered situation. It equals ln (2) and it is depicted so (Figure 3).
Speculations on the disputable results are conducted in a few directions. One portion of the discussion it is a grounding of the developed multi-optional approach adequate application to the psychophysics processes.
Accordingly to the previous works discussions [1-4], the principal question has been remained unsolved: “Why do we logarithming external stimuli?” The stimuli logarithms appeared as a result of the differential equation (3) integration (Equation (4)) at the initial conditions expressed with Equation (7). The concept was entirely composed upon the principles that differences in stimulus and its perception are proportional to one the other (Equation (1) and (2)); and that was accepted since it was justified with many evidences (experiments). However, in actual fact it is just a statement of a real situation rather than scientific explanation of the situation roots. The question: “Why all that is so?” This presented work clearly answers. We treat the stimuli (subconsciously/not deliberately/in spontaneous manner) as options in optimal way with taking into account the degree of the options uncertainty. This provides corresponding perception (response), which happens to have the properties, discovered a long time ago and still being under consideration and search for a satisfactorily scientific explanation. One of possible substantiations is the attempt taken in this paper. The comparison of the mathematical derivation results for both traditional: Equation (1)-(9), and proposed herewith alternative: Equation (10)-(20), methods shows the results identity. Therefore, the proposed way of the Weber-Fechner law derivation is at least adequate to the objectively existing and empirically established situation. It is visible in Figures 1-3 that threshold values expressed with the accepted equation (7): 
are satisfied and coincide for all ways of determination. Moreover perceptions as the functions of stimuli and hybrid optional stimuli functions are also coincide within the entire range of the stimuli variations (Figure 2). That is not only for the calculation data values (26). The equalities of equations (27) prove that as well as are firmly saying that our perception of the initial stimuli and normalized hybrid optional stimuli functions are identical (Figure 2). The threshold values appear at the hybrid optional functions entropy maximal value (Figure 3). The modified multi-optional hybrid approach discussed herewith also differs from the traditional subjective analysis SEMP as here we do not imply any preferences functions determination through known effectiveness functions; rather we determine unknown perception (analogue to effectiveness functions) through given stimulus, optimizing a similar to SEMP objective functional [7] although. Furthermore, the procedure described with Equations (15)-(20) as well inevitably leads to the law of subjective conservatism introduced in paper [10] but also without subjective preferences.
The proposed multi-optional method of the Weber-Fechner law derivation implies a functional value optimization with respect to the optional hybrid functions measure of the functions uncertainty degree as their entropy.
With the help of the approach that results in the law of subjective conservatism there has given substantiation to stimuli logarithming in order to retrieve perception. Further research is worthy in the field of optimization principle allowing finding the extremal stimuli distributions for obtaining perceptions, being at the same time delivering the extremal value to the purpose functional.
