Review Article - (2015) Volume 6, Issue 2
Objective: To use multivariate statistical analysis to process the electroencephalographic (EEG) signal recorded
during the solving of language and mathematics tasks by two groups of children, with (LD) and without (NO) learning
disabilities, and thus, to understand the possible difference in the neural circuit organization between these two
groups.
Methods: We processed the EEG data using an algorithm that summarize all the information about the possible
sources of the EEG signal, recorded by each of our 20 electrodes, into a unique variable. Factor Analysis (FA) was
used to study the covariance of this variable and Linear Discriminant Analysis (LDA) to separate samples of distinct
groups.
Results: FA disclosed 3 factors to group NO and 2 for group LD. The electrodes, grouped on each factor of each
group are quietly different. LDA disclosed a frontal/posterior differentiation between NO and LD groups, grouping
mainly the frontal and central electrodes on NO group and the occipital and posterior temporal electrodes on the LD
group.
Conclusion: Results clearly differentiate both groups of children, showing a stronger participation of (pre)frontal
and central regions of the brain on normal children, whereas learning disabled children showed the use of frontal,
temporal and occipital areas.
Keywords: Electroencephalogram; Brain mapping; Dips; Factor analysis; Linear discriminant analysis; Learning disability
Neurodevelopment disorders are experienced by at least 10% of school-age children being important causes of school evasion [1-9]. Specific impairment of oral and written language, dyslexia, dyscalculia, attention deficit and hyperactivity disorder (ADHD), social dysfunction, oppositional defiant disorder and conduct disorder are among the most common neurodevelopment disorders [4,6,9,10].
Both, genetic and environmental factors are associated with these neurodevelopment disorders [1,4,5,8,11-19]. There are clear evidences that specific language impairment and dyslexia are genetically associated with neurodevelopment disorders [6]. However, Tomblin, Smith and Zhang [19] have found that parental education, tobacco smoking and breast feeding were also related to differences between normal and affected children. Specific language impairment may interfere with social cognition [9], but social dysfunction is also dependent on genetics [13] and environment [4]. Conduct disorders and ADHD are associated with dysregulation of frontal-subcorticalcerebellar circuits [1,3] promoted by genetics [13,17], as well as pre and post-natal events [4,18,19]. Prenatal stress and childhood maltreatment predict individual differences in cortisol in the first day of school and in pre-adolescent children [20,21], influencing the development of the hypothalamic-pituitary-adrenal and serotonergic systems.
We suppose that the cognitive tasks presented to the children in school, for instance reading and calculating, will be solved not by some specific brain area, but by the combination of those most suitable neurons. In other words, according to its connectivity, membrane properties, and DNA-protein reading, each group of neurons will be or not part of the neural processing responsible for the solution of the task, and those involved will be recruited in specific time and for a specific duration. It means that the solution of the tasks are not dependent on isolated brain areas but by the neural network connectivity modulation [22,23]. All the brain is a complex system of information processing and behavior generation. Every millisecond our neurons may be receiving or transmitting (firing) electrical impulses by means of ion changes between the inner matter of the neuron and its surrounding environment [24,25]. We believe that what really change over time, during any task solution, is how each group of neuron is firing or is being fired, by alteration of the frequency of its firing.
Aiming to use the EEG information, not to look for specific brain area activation, but to understand how the different areas of the brain may be connecting each other during each moment of any cognitive task solution, we developed an algorithm based initially on the Distributed Intelligent Processing System (DIPS) theory. DIPS was first developed in the field of Artificial Intelligence to formalize systems comprised of multiple agents that have individual expertise in solving defined problems but gain the ability to solve tasks of greater complexity through cooperation. DIPS intelligence is, therefore, a function of the types of tools used by its agents, as well as how and for what purpose these tools are used [26-30].
More specifically, we may propose that in the brain, DIPS knowledge is distributed among its agents or neurons according to their specialization, and is primarily encoded by the relationships or connections shared by these agents or neurons. In the case of memory, for instance, some agents (e.g., sensory neurons) are responsible for storing data (e.g., sensory information) while others (e.g., hippocampal neurons) keep track of the relationships between these pieces of data by storing information about the associations between these agents (e.g., connecting the different sensory neurons). In the case of procedural knowledge, some agents relate data (e.g., sensory or memorized information) to their processing tools (e.g., motor actions). If we take the above assumptions, the complexity of a DIPS knowledge in the brain will depend on the number of specialized neurons, but most of all on the complexity and versatility of their connections.
Task distribution is an interactive process between an agent with a task to be executed and a group of agents that may be contributing to task execution. Many of these agents may propose similar but not identical solutions to a given task, either because they may share information from different sources or because they use different tools to handle the same piece of information. This redundancy supports the robust degradation properties of DIPS because agents may be lost without greatly affecting the system’s performance. However, this same redundancy may also cause conflict, which, in turn, requires task solutions to be carried out under the guidance of special rules implemented by specialized agents [7,28,31].
Two sample groups of children were selected. One from a public school of the city of Mogi das Cruzes (Sao Paulo, Brazil), having learning difficulty complaints by their teacher, a history of negative factors during pregnancy and deliverance, disclosed by a anamnesis, and a continuous (more than 6 months) lower performance in standard academic tests than expected for their school age. The other group was selected from a private school on the city of Sao Paulo, where none of the students had neither learning difficulty complaint, nor negative occurrences on the anamnesis, and all accomplished with the academic tasks of their grade.
LD group was composed of 42 students and NO group of 24 students. The age of the LD children has varied from 10 to 14 and of the NO children from 8 to 12. This age difference occurred owing to the school gap of LD children. All children in this study had a consent form signed by their parents and saved on the schools.
Here, we propose the use of multivariate statistical analysis to process the electroencephalographic signal recorded during the solving of a set of language and mathematics tasks by two groups of children, one with learning disabilities (LD) from a community in condition of social and economic vulnerability, as considered by the municipality authorities, and other with no learning difficulties (NO) from a regular community. A small sample of these groups was already studied in our previous work focusing on reading skills [26].
Children solved the tasks while their EEG signals were registered using 20 electrodes placed according to the 10/20 protocol; impedance below 10 Kohm; low-pass filter 50Hz; sampling frequency of 256 Hz and 16 bits of resolution. Statistical analysis of their performance and the recorded EEG signals provided the data to investigate the linguistics and mathematics abilities, generating whole brain mappings based on the entropy of each EEG electrode [26,27,32] and on non-supervised and supervised multivariate techniques. The technique of EEG summarization is not new and has been successfully applied to study neural plasticity [32], arithmetic brain processing [27], dermatological treatment satisfaction [33], election decision making [34], DIPS model [35] and, more recently, moral dilemma [36], medical diagnosis [37] and reading process [26].
Both groups had to solve different kind of tasks in Portuguese written language and mathematics. Portuguese tasks included word and phrase reading while mathematics included quantity/algorism association, sum and subtraction of tens and unities.
The activity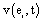
recorded by a set of electrodes ei is a weighted sum 
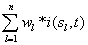of the electric currents i(sl ,t) generated by different sets si of source neurons that are being activated at different cortical areas at time t. Correlation analysis of the electrical activity v(ei ,t ) recorded by the different electrodes ei may be used to summarize information provided by each electrode ei about all involved sources si into a single variable.
The correlation coefficient ri,j calculated between the activities,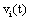 
, 
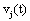recorded by ei , e j is expected to be highly dependent on the wi , w j weights determining the contribution of sl to these recorded activities. If wi , w j are high, then source sl is an important determinant of both vi (t) and v j (t), increasing the determination coefficient r , whenever it is active. If two different sources sl , sm are influential upon ei , e j respectively, then ri,j approaches 1 or -1, if they are positively or inversely correlated. The closer the coefficient is to either −1 or 1, the stronger the correlation between the variables. Because of this, the determination coefficient
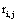of the correlation calculated for v(ei ,t ), v(e j ,t )is, here, equal to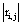 
The determination coefficient 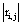increases if sl , sm are either near to both ei , e j or are synchronized. In contrast, if all sources that are influential upon vi (t) , v j (t) are silent, then 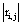approaches 0.5. In this theoretical context, the highest uncertainty about the information provided by ei , e j about sl and sm occurs when 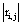approaches 0.5, and it is minimum when 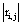approaches 1.
Because of this, Rocha et al. [27,32,35-37] proposed that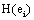 
provided by ei about the sources sl is the expected value 
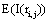of the information 
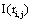provided by 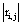The amount of information 
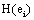provided by electrode ei about the sources sl is assumed to be a function of the determination coefficient ri, j of the correlation between v(ei ,t ) and v(e ,t ). Now, in the same line of reasoning used by Shannon [38] to define the amount of information provided by a random variable, it is proposed that the informational equivalence
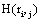, is calculated as:
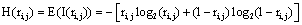(1)
such that if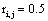 
then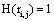 
and if 
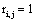or 
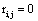hen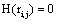 
Now, given
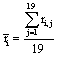(2)
the informational equivalence measured by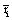 
is calculated as
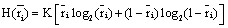(3)
and it quantifies the information provided by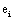 
concerning that provided by all other 
.
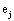Finally, the quantity of information provided by ei about the sources si involved in solving the present tasks is calculated as:
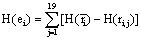(4)
In this context, the information H (ei ) provided by electrode ei about the sources sl activated for task solution is calculated from all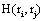 
in comparison to H (ri ). If 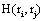is equal to the mean information 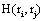provided by all other (19) electrodes e j, then v(ei ,t ) compared to v(ej ,t ) did not reduce the uncertainty about sl being involved in the task solution. In contrast, if 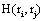approaches zero, then all fundamental sources sl for the activity recorded by ei are most likely involved in the task solution. In this line of reasoning, H (ei )measures the information provided by the electrode ei about all sources sl activated by a given cognitive activity. Thus, H (ei )provides information about the spatial and temporal distribution of these sources sl, showing how different sets of neurons may enroll themselves in a widely distributed network to solve a task [35]. Another interesting H (ei ) property is that it summarizes information about all sources si into a single variable, simplifying further analysis (factor and linear discriminant analysis) involving behavioral and neural variables.
Figure 1 shows an illustrative example of an EEG summarization calculated in the experiments for the C3 electrode.
Figure 1: An illustrative example of an EEG summarization calculated in the experiments for the C3 electrode. All the calculations have been made using the previous 2 seconds immediately before the decision making.
Factor Analysis
We have used Factor Analysis (FA), a well-known multivariate statistical technique, to describe the association between the entropy values of the electrodes in a nonsupervised way. The main idea behind FA is to disclose the relationships among the original variables using a few unobservable random ones, called common factors, to adequately represent the data [39].
In particular, let a Nxn data matrix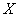 
be composed of input N signals (or trials) with n variables (or electrodes). This means that each column of matrix 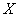represents the EEG summarization of a particular electrode H (ei ) observed all over the N trials [26]. Let this data matrix X have sample correlation matrix R with respectively Ρ and Λ eigenvector and eigenvalue matrices, that is,
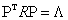(5)
It is a proven result that the set of m (m ≤ n) eigenvectors of R, which corresponds to the m largest eigenvalues, minimizes the mean square reconstruction error over all choices of m orthonormal basis vectors [40]. Such a set of eigenvectors, scaled by the square root of the corresponding eigenvalues [39], and calculated as:
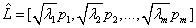(6)
is known as the factor loadings of the data matrix 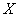estimated by the principal component method.
The estimated factor loadings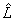 
of 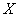can be rotated in order to improve the understanding of the factors. In this way,
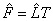is a n × m matrix of rotated estimated factor loadings, where T is assumed to be an orthonormal m × m rotation matrix. Ideally, we would like to see a pattern of loadings where each subset of electrodes is highly represented by a single factor and has negligible coefficients on the remaining ones, allowing an interpretation of the EEG brain mappings with no overlappings. Thus, our natural choice of the orthonormal matrix T has been based on the varimax criterion proposed by Kaiser [41], which has been followed by others in analogous works [7,27,32,34].
Therefore, those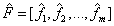 
can then replace the initial n variables on m rotated common factor loadings where not only the association between the EEG electrodes would be most expressive in terms of variance information, but also the brain mappings would be the most independent ones given by the perpendicular rotation T.
The association between the entropy values of the electrodes H (ei ) in a supervised way has been performed here using Linear Discriminant Analysis (LDA) and the technique of hyperplane navigation [42-44]. The primary purpose of LDA is to separate samples of distinct groups by maximizing their between-class separability while minimizing their within-class variability. Let the between-class scatter matrix Sb be defined as
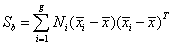(7)
and the within-class scatter matrix Sw be defined as
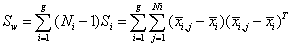(8)
where xi, j is the n − dimensional signal (or trial) j from class π i , Ni is the number of trials from class π i, and g is the total number of classes or groups. The vector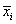 
and matrix Si are respectively the unbiased sample mean and sample covariance matrix of class π i [40]. The grand mean vector 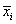is given by
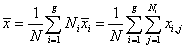(9)
The main objective of LDA is to find a projection matrix Wlda that maximizes the ratio of the determinant of the between-class scatter matrix to the determinant of the within-class scatter matrix (Fisher’s criterion), that is,
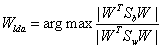(10)
The Fisher’s criterion described in equation (10) is maximized when the projection matrix Wlda is composed of the eigenvectors of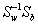 
with at most (g − 1) nonzero corresponding eigenvalues [40,45]. In the case here of a two-class problem, the LDA projection matrix is in fact the leading eigenvector Wlda of .
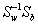Once the leading eigenvector Wlda has been computed, we can move along its corresponding projection vector and extract simultaneously the discriminant differences captured by the entropy of each EEG electrode. In mathematical terms, assuming that the spreads of the sample groups follow a Gaussian distribution, this procedure of navigating on the most discriminant projection [44] can be generated through the following simple expression:
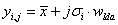(11)
where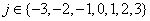 
and σ i is the standard deviation of each sample group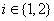 
A specific anamnesis, which involved the relatives of the children, was used on a previous moment to investigate the possible neurological disturbance of the LD sample group. This anamnesis considered environmental factors that could have impaired brain development from the fetal age until early childhood. The LD group particularly exhibited statistical significant occurrences such as motherly high stress index during pregnancy, use of tobacco and alcohol, low birth weight, among others, suggesting their difficulties in learning due to possibly neurological disturbances.
Principal Component Analysis (PCA) was used to study the covariance of the variable H (ei ) calculated from the data generated by the coordinate activity of neurons belonging to the distinct neural circuits involved in solving a cognitive task, being each of these circuits, as proposed here, represented by a distinct component of the PCA analysis which eigenvalue is higher than 1. Running the Factor Analysis in the space of variables H (ei ) grouped by the PCA, we maximize the covariance between those electrodes of each component by means of its eigenvalue. Finally, using the Varimax rotation, we are able to better disclose the association between the EEG electrodes supposed to be associated to each neural circuit.
Figures 2 and 3 describe the rotated estimated factor loadings of the neural organization of the NO and LD sample groups, respectively.
Figure 2: Brain mapping of the most expressive factor loadings (red to blue) of the NO sample group with corresponding eigenvalues greater than 1.
Figure 3: Brain mapping of the most expressive factor loadings (red to blue) of the LD sample group with corresponding eigenvalues greater than 1.
In NO group Factor Analysis disclosed 3 factors with eigenvalue higher than 1, while NO group disclosed 2 factors with eigenvalue higher than 1. The first NO factor associated bilateral electrodes on occipito-temporal regions (T3, T5, T5, T6, O1 e O2) and PZ, while NO group second factor disclosed frontal-central areas bilaterally (FP1, FP2, F3, F4, F7, F8, Fz, C3, C4, Cz), and finally third factor disclosed just the medial occipital and parietal electrodes (Oz, Pz).
Factor Analysis on LD group entropy values grouped, on the first factor, electrodes on occipital and posterior temporal regions (O1, O2, T5, T6), besides medial parietal area on Pz. The second factor disclosed the association between frontal and temporal areas bilaterally (F3, F4, T3, T4) plus right central electrode C4.
Lastly, the Linear Discriminant Analysis (LDA) brain mapping is shown in Figure 4. Factor Analysis looks for the most expressive association between the EEG electrodes in terms of variance information in a non-supervised manner, but it does not disclose the variables that discriminate the most between possible different groups of individuals. So we brain mapped the LDA eigenvectors calculated for both group of children (LD, NO), showing the regions of the brain which activity may had discriminate the most between student with and without learning disabilities.
Figure 4: Brain mapping of the most discriminant entropy values (red to blue) captured by the LDA hyperplane navigation. From left (group of NO samples) to right (group of LD samples).
LDA hyperplane navigation has disclosed a frontal/posterior differentiation between NO and LD, grouping mainly the frontal and central regions of the electrodes T3, C3, F4, C4 on NO group and the occipital and posterior temporal regions of the electrodes Oz, O2, T5 and T6 on the LD group (Figure 4).
Increased EEG power in the theta band at rest (4–8 Hz) is one of the most consistent and robust neural abnormalities in ADHD [46]. Decreased levels of absolute beta and gamma power were also identified in ADHD children, compared to controls [47]. Answering to visual and auditory continuous performance tests, ADHD patients showed significantly higher theta relative power, lower beta relative power, and higher theta/beta ratio. These results led the authors to propose that cortical hypoarousal effects on the fronto-striatal circuitry may be implicated in the inhibition of premature responses [48].
On the study of Hasko et al. [49], control group revealed greater activity over left fronto-temporal electrodes, whereas the N300 ERP component was distributed bilaterally in the group of children with dyslexia. Compared to control children, dyslexics also showed lower amplitude of parietal, occipital, and temporal alpha 2 and alpha 3 sources [50].
Soltész et al. [51], on their work about dyscalculia, found between 400 and 440 ms a focused right-parietal ERP distance effect in controls, but not in children with dyscalculia during digits identification. Soltész and Szucs [52], using temporal principal component analysis on ERP data, found hemispheric differences in the first temporal component and group differences in the second temporal component, suggesting executive control differences between children with dyscalculia and controls.
All these works and many others exhibited differences between normal and learning-disabled children in terms of brain regions dysfunction measured by its frequency domain or its ERP response. Here, we first processed the EEG data using an algorithm that considers the brain as a complex network comparable to a Distributed Intelligent Processing System (DIPS), summarizing thereby all the information about the possible sources of the EEG signal, recorded by each of our 20 electrodes, into a unique variable H (ei ), corresponding to a 2 seconds window of cognitive processing.
While Factor Analysis disclosed 3 factors (Figure 2) from NO group H (ei )data, it found just 2 factors (Figure 3) from LD group. Each factor is supposed to represent a specific neural circuit. Thereby, we may assume that NO group organized its neural network on 3 distinct manners consecutively, while LD group did it only on 2 distinct manners. Here, we replicated our results from a smaller sample of these same groups on reading tasks [26], where we also found 3 factors for the control group and only 2 for the learning-disabled children.
Other difference between the neural networks of both groups is how each factor is composed. While NO factors show the association between (pre)frontal and central areas, LD factors show association between frontal, temporal and occipital areas. Studying frequency domain analysis, Fernández et al. [53] found that their control group showed greater power increases in frontal regions than the learning disabled group, in the frequencies between 1 and 6 Hz from 300 to 700 ms. LD children also showed shorter durations, than the control group, of the decreases in power of alpha and beta rhythms in the occipital regions in frequencies between 8 and 17 Hz from 450 to 750 ms. Authors interpreted it as a deficit in attention and memory retrieval.
Linear Discriminant Analysis
From our LDA results, it may be proposed that what most discriminate the normal group from learning disabled children is activity over frontal and central neural circuits, whereas LD group may be discriminated by a more posterior activity (Figure 4). Hämäläinen et al. [54] found that children at risk for reading problems, compared to control children, showed a negative voltage shift at 107–215 ms in frontocentral areas, the difference being originated from the left and right auditory cortices.
