It is generally accepted that physical exercises have a good impact upon an individual health including her/his psychic status [1-5]. Though, according to exercises realization and consequences they may be classified or distinguished as developing, supporting, and degrading. All that is because of the balance between (and combinations of) the fatigue accumulation effect and exceeded, complete, and incomplete corresponding restoration levels of muscles and tissues (skin, vessels, organs, etc.) [2].

Physical exercises are purposed at developing or improving related qualities and skills such as, for example, psychological state, reaction, speed, stamina, strength, sharpness, other characteristics. These all and corresponding exercises, and modes of their execution, and combinations of all that with the parameters of the exercises are alternatives mentioned at [1-6].

Finally, there are groups of muscles: fast, intermediate, and slow for restoration which predetermines a multi-alternativeness of the expected training process as well and that also stipulates uncertainty at making a decision about necessary exercises [2].

An important matter here is subjective preferences of the physical exercises [5] because motivation is a powerful psychological factor that may accelerate remedial effects of the exercises and highlight apparently possible troubles that may occur in the process of the physical exercises practicing implementation [1-6].

The presented paper is about several proposed models for the subjective preferences determination that might also be applicable in some other areas of psychological activity, e.g., for requirement strategies elaboration [6].

The subjective entropy maximum principle (SEMP) proposed and developed by Professor Kasianov (National Aviation University, Kyiv, Ukraine), [7-17], was put down into the foundation of this work.

The proposed models parameters might be interpreted, e.g., as a heartbeat rate (HBR), speed, intensity of the physical load, the scope of the load itself, extensity, duration, periodicity, frequency, time, their combinations etc. gathered into cognitive functions.

Let us consider a few models of physical exercises influence upon a psychic state of an individual (patient, athlete, professional or amateur etc.). It is obvious, physical exercises differ in intensity, periodicity (frequency), scope, magnitude, sequences, durations, designations in goals and so on [2]. Also it is clear, their impact depends upon an individual fitness, age [1,3], time and quality of restoration as well as the physical exercises differences mentioned above, psychological type and many other personal subjective characteristics of the trained patient.

Moreover, prescriptions for one or another physical exercise as a remedy must take into account all that stuff and therapeutic effectiveness for a specified illness healing with respect to the patient’s subjective preferences for that exercise. Thus, patient’s psychology may be considered both the aim for the cure and a backward indication of the conducted medical treatment (by means of the physical exercise) success.

Generally psychic state may be expressed or denoted as y function dependent upon some also generalized, in its turn, value

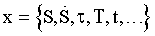------      (1)

where S – scope or magnitude of the carried out physical exercise load (measured, for example, in miles or laps run at a sports ground, miles swum at a swimming pool, number of weights lifts done at a gym etc.);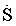– intensity of the physical exercise performing (e.g., speed of run or swim, number of lifts per a unit of time, the same to the number of pull-ups at a gymnastic bar, push-ups, sit-downs, stand-ups, … , all that has to be educed to the time of their execution), i.e. the first derivative of the value of S with respect to time t ; τ – duration of the exercise practising; Τ – periodicity of trainings; t – time itself.

Expression (1) implies a relation between a set of studied parameters 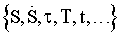and the value of y impacting the patient’s psychology function y.

A model of physical exercise impact upon patient’s psychology function effectiveness

In some cases of a phenomena being studied we cannot establish the direct dependencies or relations between corresponding parameters expressed in a certain quantitative form.

But, fortunately we are sometimes lucky to discover or justifying reveal the dependencies or relations between quantitative changes of the corresponding parameters which makes it possible to find or derive the sought dependencies.

For instance, if it is established that the rate of the patient’s psychology function y change: d_y with respect to the value of x change: x is proportional to the difference between the value of the patient’s psychology function y and its “normal” level n_l : y − n_l , then it gives the model of the wanted dependence of y(x) in the view of the differential equation:

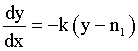     (2)

where k – coefficient of proportionality.

Equation (2) has a well known solution:

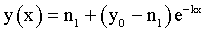     (3)

where y₀ – initial value of y at the initial value of x = 0 .

Here, in Equations (2), (3), at 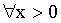, if 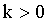, y → n_l if x → ∞ ; k = 0 ,y ≡ y₀ and if k < 0 , y → ∞ if x → ∞ .In the considered problem setting, the coefficient of proportionality k symbolizes the effectiveness of the value x , expressed with the help of (1), impact upon the patient’s psychology function y : Equation (3), in the framework of the model expressed through the differential equation (2).

In some respect parameter k can be interpreted in terms of subjective analysis as a preference function in regards with the corresponding alternative. These models are going to be considered in the following subsections of the paper.

A model to take into account subjective preferences of discrete alternative physical exercises

Subjective analysis [7-17] offers a great variety of models for taking into account multi-alternativeness of an individual’s choice by means of subjective preferences functions distributions on conditions of uncertainty.

Let us apply a psychological purpose functional 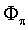, [8,16,17], to describe the value of x expressed with (1), i.e.

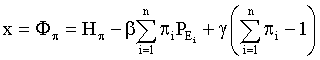       (4)

where H_π – measure of uncertainty, subjective entropy, of an individual preferences π_i :

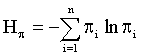      (5)

n – number of achievable alternatives (discrete physical exercises, e.g., running, swimming, stretching, pulling-ups, pushing-ups, lifting weights etc.); β – endogenous parameter of the individual’s psych (psychic temperature); 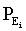– corresponding physical exercise effectiveness function (cognitive, utility function); γ – uncertain Lagrange multiplier for the normalizing condition:

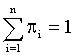        (6)

In this problem setting, in the functional (4), if β > 0 at 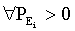, it is modelled that the individual prefers the minimal values of functions of 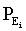more. If β < 0 , 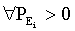she/he seeks after the 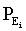maximal value.

The SEMP [7-17] application gives the desired individual’s preferences distributions in the so-called canonical view [8,1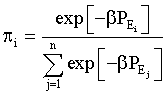7].

        (7)

A model to take into account the density of the subjective preferences distributions for a continuous alternative physical exercise

This model implies existence of a physical exercise as a continuous alternative, for instance, it might be the distance continuously being run or swum, the time of an exercise which is being performed, i.e. an alternative which preference by a patient can be described with her/his subjective preferences densities distributions.

For such model we propose the one similar to functional (4) but in the integral view, [10-12,16]:

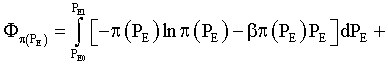
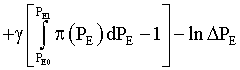       (8)

Here, in Equation (8) P_E represents the uninterrupted parameter of the continuous alternative considered as the corresponding subjective effectiveness function and independent variable for the problem setting (e.g., HBR). ΔP_E – degree of accuracy at the entropy determination.

The optimal subjective preferences densities distributions π(P_E ) are obtained on the basis of SEMP, [10-12,16]:

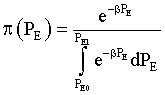       (9)

This type of models is a step of a generalization of the previous models kinds and it takes into consideration, for instance, a few separate alternative physical exercises (e.g. running, swimming, rowing etc.) which have a common parameter (let us say the distance coped, HBR or quantity of calories burnt) that may vary continuously for each of the discrete alternatives.

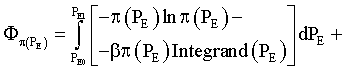
Thus, we come to the model applied in 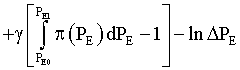[10]:

         (10)

where Integrand(P_E) – integrand of the conditional view, in case of some three discrete alternatives it is [10]:

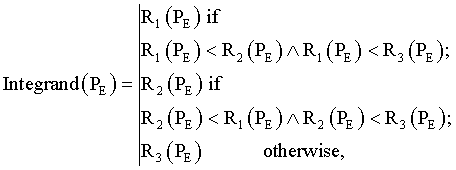           (11)

where R_i – subjective effectiveness functions corresponding to the discrete alternatives.

Applying SEMP to functional (10) with respect to conditions (11) it yields the required solution (optimal subjective preferences densities distributions) in the view of [10]:

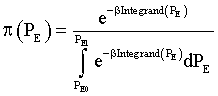          (12)

Models to take into account the uncertainty average value for a diapason of discrete physical exercises alternatives preferences assessing

The purpose functional in such problem setting combines elements of functionals (4), (8), (10), [7]:

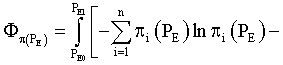
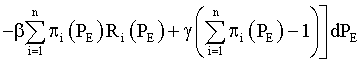              (13)

Let us consider the expression of [7]:

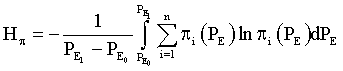              (14)

The expression of (14) can be interpreted as a mean value of the uncertainty characteristics existing within the interval of 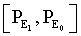, [7]. It relates with the “instantaneous” subjective entropy denoted as above with the formula of [7]: Equation (5).

The optimal solutions for functional (13) has the canonical view of [7]: Equation (7):

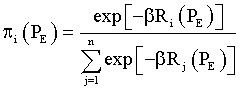             (15)

A particular model for inseparable discrete physical exercises alternatives

The parameters sometimes can be undividable and there can be time amongst them. The proposed model, for example, in the two alternative case with cognitive functions of t and t , has the view of

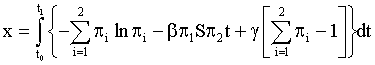           (16)

The use of SEMP in case of (16) gives

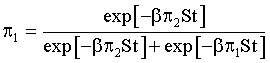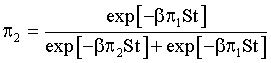,           (17)

As we see the preferences of Equation (17) cannot be expressed in the explicit way, however their system might have solutions. The solutions of Equation (17) system must satisfy the expression

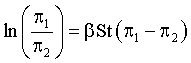           (18)

This, Equation (18), is the well known Weber-Fechner law of psychology or Jakob Bernoulli law in economics, also derived on the basis of SEMP in [14], applicable here, in the considered problem setting, as the case when a stimulus of a physical exercise (motivation for the physical exercise doing accordingly described with the parameter) is simultaneously a perception of it (readiness or willingness to execute the exercise assessed with the parameter), besides both the stimuli and their perceptions are measured and expressed in subjective preferences π_i.

The results of numerical simulation are going to be presented and discussed below. Here we will just briefly mention the necessity of distinguishing the physical exercise alternatives and their related parameters of S and t with the corresponding subjective preferences π_i.

Thus, for such problem setting we need some kind of a “selective product” for mathematical logics operation “and”.

A few more models for cognitive functions and psychological purpose functionals of physical exercises alternatives

In functional (16) it is used a cognitive/effectiveness function in the view of

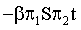           (19)

Other possible combinations of the utility/effectiveness parameters of the related alternatives with respect to the studied psychological phenomena would be, instead of expression (19)

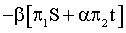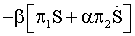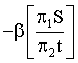;;           (20)

where α – corresponding coefficients for equaling the differences in the parameters and functions measurements units.

The latter of the expressions (20) has a meaning of the generalized average speed (possibly HBR), i.e.

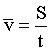         (21)

with respect to the two of its components separately, although.

The solutions for optimal preferences distributions in a case of the cognitive function given with the last of the expressions (20) are obtained from the equation

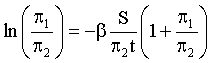        (22)

More combinations and variants of related to corresponding alternatives cognitive functions are considered [7]. There, the application of SEMP yields optimal solutions also for the effectiveness functions which can be interpreted as the optimal mutual impact between the psychological parameters and physical exercises in multialternative situations.

For a psychological purpose functional we might consider the following expression:

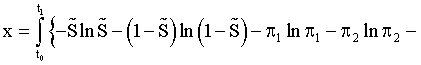
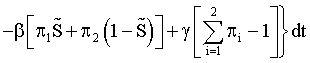        (23)

where 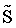– special utility/effectiveness/cognitive dimensionless function (possibly ratio, normalized score), allowing mathematically logarithmic operation, has been got by the physical exercise in the patient’s opinion in conditional units (CU).

The extremal solution for the effectiveness function yields

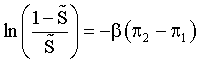        (24)

the exact mathematical expression of the Weber-Fechner or Jakob Bernoulli law, where 1−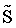 and 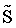– stimuli in CU; π_i – their perceptions.

The extremal solution for the preferences yields

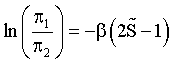     (25)

The results of the mathematical models computer simulations for the presented methods Equations (1)-(25) are illustrated in Figures 1-5.

Figure 1: Optimal distributions of a physical exercise preferences.

Figure 2: Optimal distributions of a physical exercise preferences change at the variation of a parameter.

Figure 3: Areas and contour lines of a physical exercise preferences change at the variation of a parameter.

Figure 4: Iterations for optimal preferences determination.

Figure 5: Optimal preferences solutions.

The models of Equation (1)-(3) give obvious solutions; an interested reader can easily plot corresponding diagrams independently. Concerning Equation (4)-(15) there have been performed a lot of simulation described in [7-17]. For the case of Equation (16)-(18) and accepted values of

β = 0.0693; S = 5.4 ; t = 9.9      (26)

all values in CU, the results are illustrated in Figure 1. In there: p1 designates π₁ ; p2(p1) is for 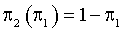; the diagrams are drawn in the denoted at the plot scales in order to be presented conveniently together for the comparison ease. The roots of Equation (18) are seen as the three knots (where all three lines intersect) with the preferences values of 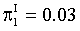;;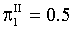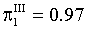. Corresponding coordinates are, for the knots: I – (0.03,−0.94037) ; II – (0.5,0); III – (0.97,0.94037) . These values are denoted in Figure 1.

When the parameter of S can have variations we get the picture shown in Figure 2. Here it is designated N(p1,...) as the value of Equation (18).

Here it is visible the change of the physical exercise preferences optimal values in accordance with the parameter of S variation. The process’s curves shape resembles the well known van der Waals curves of condensation, boiling, and evaporation for liquid-gaseous and vice versa transformations of aggregate states in thermodynamics. In the three dimensional contour plot shown in Figure 3 it is easy to notice the similar process, i.e. the preferences “evaporation” and “condensation”.

The iterative procedure shows that for 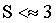CU there exists the only solution 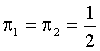, there is a straight line vertical fragment marked “0” (see Figure 3). For 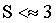we observe the three solutions also visible in Figures 1 and 2. These are 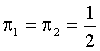and other two positioned on the curve marked “0” (see Figure 3). In this area the slightest diversion from the solution of 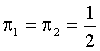leads to either “evaporation” through the psychological “overheating” of the preferences deflected or “condensation” by means of “overcooling”, depending upon the side of the preferences displacement and having been chosen distinction between them. It is shown in Figure 4. Thus, we have found some kind of “a psychological threshold” for the parameter of S .

Similar results can be obtained for Equation (22). It is represented in Figure 5. The accepted above data Equation (26) has been changed for experimenting purposes with the value of the endogenous parameter of the individual’s psych

β = −0.0171 ^CU (27)

The models and results of simulation induce disputes in regards with several issues. First of all it is grounding of the models. Then, it is assessment and identification problem of the models parameters. After that, it is interpretation of the results.

Concerning the substantiation of the proposed models it has to be said that they do not distort the objectively existed dependencies and their optimal values. Human-beings do process the external information, in the view of physical stimuli, as alternatives of the models, resulting that process in sensations, perceptions or preferences of these methods. Laws of psychophysics can be derived on the basis of SEMP [13,14]. Science evolution uses two ways to develop knowledge: building a system of non-contradictable, due to their obviousness, axioms then deriving and proving theorems; and postulating some reasonable principles which application leads to results that do not contradict with the practice. The latter way is tried to be used in the presented paper.

Talking of the problems of the models parameters identification and estimation, a clinical or experimental researcher needs collecting statistical data for approximation those considered parameters of the described above models Equations (1)-(27).

Also, there arises a problem of distinguishing the physical exercise alternatives and their related parameters.

For the interpretation it seems important that in all above considered cases 0 < π < 1 for any preferences functions of the corresponding alternatives in spite of their corresponding cognitive functions might be “zero” assessed with the subjective value or utility, i.e. at the P_E = R = --- = S = t = --- = 0 but taking into account those alternatives, it means keeping them (those alternatives) in patient’s mind anyway. When some π = 0 it means the corresponding alternative is not considered at all, i.e. it does not enter the set of the attainable alternatives or is just ignored by the patient. At last, if some π = 1 , it means the problem is not alternative at all any more since according to the normalizing condition Equation (6) the sum of all other preferences functions equals zero and it turns for each of them π = 0 which in its turn ruins the mathematical sense and structures of the psychological purpose functionals Equations (4), (8), (10), (13), (16), (23) and similar [7-17]. The mathematical operations similar to logics “and” and “or” apparently need to be created. It is for the purpose, for example, of distinguishing alternatives’ parameters, cognitive functions, corresponding preferences etc. in product expressions, which describes the selections, grouping of parameters, and orders of operations in those products (e.g., see Equations (16)-(18) and expression (19)).

The same is perhaps to the sum cognitive functions.

The result illustrated in Figure 2 can be obtained by the corresponding variation of any of the three parameters of Equatuion (18) βSt or of their combinations since they enter Equation (18) as the product.

The functionals Equations (4), (8), (10), (13), (16), (23) might be applied not only for every of the trained patients’ subjective preferences being obtained but also for each of her/his coaches’.

The “evaporation” and “condensation” effects for the preferences (see Figures 1-5) are phenomena that need their further investigation. It is like psychological overheating of preferences before evaporation or overcooling them before condensation.

In the area below S ≈ 3 (Figure 3) no deviation will diverse the patients mind from the maximal uncertainty; unlike at the area above S ≈ 3 – the tiniest piece of additional information may lead to not maximal uncertainty since the distribution of the subjective preferences becomes multi-alternative itself (there are three possible solutions for optimal preferences functions distribution in that area).

The “rightness” or “wrongness” of a patient’s subjective choice, expressed via her/his individual preferences of alternatives uncertainty, can be evaluated with the relative hybrid entropy function proposed in [15].

The developed approach in the framework of SEMP is an appropriate tool for modelling a physical exercise, as a remedial treatment, impact on psychology in the view of individuals’ preferences functions. Conditional entropy (uncertainty) of the alternative exercises preferences, expressed via effectiveness functions of parameters (likewise HBR or other, or in CU), collected in a corresponding cognitive functions, is a purpose psychological functional that undergoes optimization procedure. Curative effect of physical exercises is assessed by the use of the integrated, including those preferences, values. There are some areas of psychological state of a patient where there is instability in her/his individual subjective preferences. The proposed methods can be used as a diagnostic and prognostic mean. The author has experienced not once the high feeling of a deep relaxation and pacification after a good swimming or jogging and he still prefers a certain combination of them with a kayaking, fitness training and wrestling at about 120…150 HBR. In turn it makes a sense for a healthy mental work.

1. Crone D, Smith A, Gough B (2006) The Physical Activity and Mental Health Relationship – A Contemporary Perspective from Qualitative Research. ActaUnivPalackiOlomucGymn 36: 29-35.
2. Berger BG (2016) The Role of Physical Activity in the Life Quality of Older Adults. pp. 42-58.
3. Wattles MG (2001) The Role of the Exercise Physiologist in Mental Health Professionalization of Exercise Physiology. An international electronic journal for exercise physiologists.
4. Frates EP, McBride Y, Bonnet J (2016) Its Fun: A Practical Algorithm for Counseling on the Exercise Prescriptions: A Method to Mitigate the Symptoms of Depression, Anxiety, and Stress-related Illness. ClinExpPsychol S1: 116.
5. Archer T, Jansson B, Klaus Olsen (2015) Effect of Age upon Leadership Attributes from Recruitment Instrument: a Selective Developmental Trajectory. ClinExpPsychol 1:106.
6. Kasianov VA, Goncharenko AV (2015) Variational principles of subjective analysis. Modified Euler-Lagrange variational principle.
7. Kasianov V (2013) Subjective entropy of preferences. Subjective analysis: monograph, Institute of aviation, Warsaw, Poland.
8. Kasianov VA, Goncharenko AV (2013) Light and shadow. Proportions of shadow economy.
9. Goncharenko AV (2015) Applicable Aspects of Alternative UAV Operation.
10. Goncharenko AV (2014) Extremality of control and preferences distributions “goodness”. Electronics and control systems 4: 84.
11. Goncharenko AV (2014) Navigational Alternatives, Their Control and Subjective Entropy of Individual Preferences. IEEE 3rd International Conference “Methods and Systems of Navigation and Motion Control (MSNMC), Kiev.
12. Kasianov VA, Goncharenko AV (2014) Connection of Subjective Entropy Maximum Principle to the Main Laws of Psych. Research in Psychology and Behavioral Sciences 2: 59-65.
13. Goncharenko AV (2014) Some identities of subjective analysis derived on the basis of the subjective entropy extremization principle by Professor V.A. Kasianov. Automatic Control and Information Sciences 2: 20-25.
14. Goncharenko AV (2013) Measures for estimating transport vessels operators subjective preferences uncertainty. Transactions of the institute of aviation. Selected problems of air transport.
15. Goncharenko AV (2013) Expediency of unmanned air vehicles application in the framework of subjective analysis. IEEE 2nd International Conference Actual Problems of Unmanned Air Vehicles Developments (APUAVD), Kiev.
16. Kasianov VA (2007) Subjective analysis: monograph. National Aviation University, Kyiv, Ukraine.
17. Kasianov VA (2003) Elements of subjective analysis: monograph. National Aviation University, Kyiv, Ukraine.