Research Article - (2017) Volume 8, Issue 4
Objective: The physiological background for intracranial pressure, ICP, increase at brain compression is presently unknown. Current knowledge of the relationship between ICP and volume of brain compression is based on animal experiments, which has led to the theory of elastic brain tissue compression, which like a loaded spring causes the ICP increase. However, tests of brain tissue composition, or compression, find no basis for elasticity, or compression. The aim of this article is to describe the physiological features controlling ICP since it is necessary for the understanding of intracranial physiology, but also since ICP is an important parameter in neurointensive care medicine. Methods: This evaluation is based on the physiological consequences of the closed intracranial compartment, the thin-walled, compressible venous bed, the auto-regulation of cerebral blood flow, CBF, to blood pressure changes, and the coupling between ICP and the intra-capillary blood pressure through the thin, flexible capillary wall. These features influence the intracranial venous blood volume, the venous vascular resistance, and the CBF. Together these features are shown to revile the ICP dependence on the volume of brain volume compression. Results: The evaluation leads to a formula that describes the relationship between ICP and changes in the brain volume. The formula predicts an exponential ICP increase at brain compression like in animal experiments but, contrary to the elastic tissue theory, a gradually higher exponential for larger compression. Conclusion: The found relationship between ICP and changes in brain volume may prove to be a useful tool in neuro-intensive care patients for following changes in intracranial volumes by the aid of continuous ICP measurements. Since brain-compressing volumes includes the arterial pulse volume, the ICP formula may also enable CBF calculation from ICP measurements. The physiological relationships leading to the description of the relationship between ICP and brain volume change may by themselves help in understanding other intracranial phenomena, like ICP plateau-waves.
Keywords: Brain; Brain volume; Intracranial volume; Intracranial pressure; Volume-Pressure relationship; ICP Control; ICP Plateauwaves
The emerging use in 1950-60 of neuro-intensive care treatment with intracranial measurement of pressure, ICP, and decrease of intracranial volume, made the relationship between change in brain volume and ICP clinically important [1].
In intensive care patients, Ryder et al. [2] found that a rapid cerebrospinal fluid, CSF, extraction or re-infusion caused an initial rapid ICP decrease or increase, followed by a slower, non-linear return to the original ICP level.
Based on these ICP results, and animal experiments, Marmarou et al. [3] presented a model for CSF circulation with constant formation, storage in a compliance (spinal cavity?), and ICP dependent absorbtion, explaining the non-linear ICP return to original level. They also presented experimental animal (cat) data that the rapid initial ICP increase after a rapid CSF infusion depended exponentially on the infused volume for ICP up to 50 mmHg.
Brain compression, as the cause of exponential volume-pressure relationship, was tested by Avezaat et al. [4] in an experimental animal (dog) study. Inflation, ΔVic, of an extra-dural balloon compressed the brain. The recorded linear relationship between ICP increase and the curve slope (ΔICP/ΔVic) at ICP up to 60-80 mmHg supported an exponential relationship between ICP and brain compression.
The combination of brain compression and exponential ICP increase founded a theory of elastic brain tissue compression [4], which like a loaded spring caused the pressure increase.
Brain tissue elasticity at compression as the cause for exponential ICP increase was used as partial foundation for ambitious attempts to describe intracranial blood flow regulation [5], and tissue oxygenation [6], but the physical support for brain tissue elasticity is not solid.
The intracranial volume consists of CSF (water with solutions) and brain tissue (more than 80% water [7]). Water, though reshapeable, is like solid matter virtually non-compressible. Tests of the ability to compress human brain tissue, and meninges, heated to 37 degrees Celcius [8], showed no compression except a slow trend, presumably due to water evaporation since it was closely similar for all examined tissue types.
If the elastic brain tissue theory is not valid, we have no theoretical background for the observed exponential ICP increase at brain compression. Alternative theory, like the effect of auto-regulation of cerebral blood flow, CBF, [9,10] cannot by itself explain the exponential ICP increase. The aim of this study is to provide a physiological background for the relationship between ICP and brain compression.
Measurement of ICP
The distal segments of the intracranial veins are hard-walled (sinuses) that follow the inside of the cranium in three dimensions.
As a consequence of the vein lumen being kept open, gravitation effects are equal on the arterial and venous side, making regional arteryvenous perfusion pressure in the brain independent on head position.
Another effect is that the relation between venous sinus pressure and ICP is equal in all parts of the brain and also independent of head position. Consequently, intracranial pressures measurement in relation to venous sinus pressure at the same horizontal level gives physiologically meaningful results, and ICP values independent of air pressure, and of head and body position. Since the intracranial capillaries are thinwalled, and pressurized directly from the arteries, they create ICP. In effect, ICP in relation to sinus venous pressure gives the perfusion pressure for the thin-walled part of the intracranial venous system. The low resistance of the venous bed transporting intracranial blood into the superior cava vein enables mean central venous pressure, if measured at the same horizontal level as ICP, to give a close estimate of the venous sinus pressure, and to function as reference for intracranial pressure measurements.
Brain compression
Three preconditions:
1) The skull bone and the dura mater limit the intracranial volume. Since the tissue inside the intracranial volume (brain, blood, cerebrospinal fluid) is virtually non-compressible, if a new volume is introduced intracranially, it will cause the same venous blood volume to exit. If the voidable part of the venous blood volume is limited, to an amount named Vv, any volume introduced intracranially reduces Vv by the same amount:
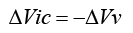
where ΔVv is the change in Vv caused by the change of the nonvenous intracranial volume, ΔVic.
2) From the capillary bed to the outflow in venous sinus the venous bed consists of thin-walled, compressible, blood vessels. The volume for the venous bed is limited, and unaffected by the intra-lumen blood pressure, Pv , but the surrounding brain tissue is reshape-able, allowing re-distribution of the blood volume. When open and not maximally distended, and surrounded by a homogenous external pressure, ICP, each venous cross-section area, depends linearly on the intra-lumen blood pressure, Pv , which gives:
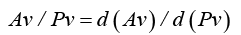
where Av is the sum of venous cross section areas with same intralumen pressure.
3) Strandgaard et al. [11] found, with CBF measurements at varied blood pressures, auto-regulation of CBF in humans, independent to variations in arterial perfusion pressure, PP (arterial pressure – ICP), in a range of about 60-160 mm Hg.
This indicates that CBF is normally independent of PP at the capillary level:
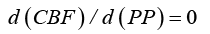
Venous resistance, Rv.
At laminar CBF, cross-segments of a blood vessel, with the length d (L) , have a resistance, d (Rv) , which is inversely proportional to the cross-segment area, Av and proportional to the cross-segment length d (L) , and the resistivity, rb (blood viscosity):
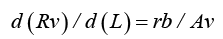
In a rigid-walled blood vessel with constant cross-section area, Av, the fall in intra-vascular blood pressure, Pv, with increasing distance, L, from the capillary bed would be in analogy to Ohm’s law for electrical current, and according to formula (4): d (Pv) / d (L) = −CBF *d (Rv) / d (L) = −CBF *rb / Av , where CBF is the cerebral blood flow.
For intracranial veins with thin, non-rigid walls, the cross-section area Av decreases with fall in intraluminal pressure, until the intravascular blood pressure, Pv, equals the surrounding tissue pressure, ICP. Insertion of formula (2) and replacement of Pv with ICP gives:
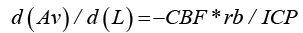
According to formula (5) Av decreases linearly with increasing distance from the capillary bed.
Formula (4) can be re-written as: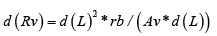 
If d(L) is increased to the whole length, Lb, of the venous bed, then ( Av *d (L)) will increase to Vv, the voidable part of intravenous blood volume, proportional to the conductance of the thin-walled venous bed, and d (Rv) will increase to R. We then get the formula:
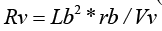
where Vv = Lb* Av (L) = Lb*( Av (0) − Lb*CBF *rb / ICP) (Figure 1) according to formula (5), and where Av(0) is the transection area of the capillary bed.
Figure 1: A schematic drawing of the intra-vascular volume in the thin-walled venous bed, illustrating the voidable venous volume, Vv.
Vv is then limited between the total venous volume (when CBF →0 ), and by 0 (when Av→0 ).
Effects on ICP
Since the ICP is the perfusion pressure for the thin-walled venous section, then in analogy to Ohm’s law, and formula (6), we get the blood flow:
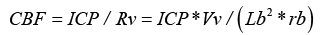
In order to eliminate CBF from equation (7) it is converted to logarithms and then derivated on by the arterial perfusion pressure PP, which gives:
d (CBF ) / d (PP) / CBF = d (ICP) / d (PP) / ICP + d (Vv) / d (PP) / Vv and since formula (3) indicates that d (CBF ) / d (PP) = 0 the equation reverts to:
d (ICP) / ICP = −d (Vv) / Vv
If the initial value of Vv is Vv(0), and the fact that Vv and ΔVic are continuous variables are considered, then formula (1) gives:
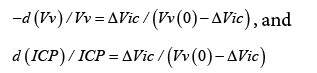
where.
ΔVic
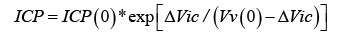
where ICP(0) is ICP, and Vv (0) is Vv , before the ΔVic reduction in brain volume.
Formula (9) is the sought relationship between brain compression, ΔVic , and ICP.
The found formula:
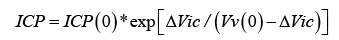
Figure 2 gives the relationship between ICP and decrease, ΔVic , in the brain volume, with one parameter, Vv(0), the voidable part of the thin-walled intra-venous volume, modifying the response.
Figure 2: Diagram of the relationship between ICP and brain compression volume increase, as given by formula (9) for ICP(0) = 6 mmHg, and Vv(0)=25 ml.
When Vv (0) » ΔVic it is obvious that the relationship between ICP and ΔVic is closely mono-exponential.
When ΔVic approaches Vv(0) the ICP slope is still exponential, but with increasingly higher exponent, until an unlimited pressure is needed to compress the brain so that Vv(0) is entirely emptied.
If the formula is re-written as:
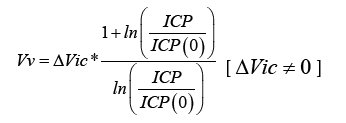
It illustrates how Vv can be measured by a ΔVic change in brain compression, and observation of the concomitant ICP change.
Since intracranial pressures derive from intra-vascular arterial pressure, it is obvious that it is the flexible, thin-walled parts of the vascular bed that influence the ICP. The capillaries are situated immediately after the last arterial segment, and the thin wall transmits their intra-luminal pressure to ICP. The thin-walled venous segment following the capillary bed is subject to independent volume reductions from increase in CSF volume, and from CBF caused reduction in intraluminal pressure. The intra-venous volume reduction causes the venous outflow resistance to increase, and a corresponding auto-regulatory increase in the intra-capillary blood pressure (and ICP) to preserve an unchanged CBF (Figure 3).
Figure 3: Equivalent electronic diagram of the present theoretical model for the relationship between ICP and brain volume decrease.
These relationships when formalized and quantified, together with the limited intracranial space, lead to the formula for the relationship between brain compression and ICP increase.
It appears from the formula that a mono-exponential relationship between brain compression and ICP increase is valid only at a neglectable compression volume compared to the voidable venous volume, as described in animal experiments [3,4] but the ICP increase remains exponential also at higher brain compressions. In hindsight, the steeper, exponential ICP increase at higher compression also is observable in early animal experiments [4].
What is the physiological function of a thin-walled venous bed? It is obvious that the volume reduction in the CBF direction eliminates any intra-vascular pressure fall. Also, the compress-ability of the venous bed enables an arterial blood volume to enter intracranially at systole, as is indicated by the ICP increase concomitant to the arterial pressure increase.
The decrease in the venous cross-section area in the flow direction, compensating for the intra-vascular pressure loss caused by flow resistance, is not limited to thin-walled intracranial veins, and it can limit the venous intra-vascular flow-dependent pressure loss also in cervical and upper body regions, improving the possibility to use the mean central venous pressure for estimation of the intracranial venous sinus blood pressure, if measured at the same horizontal level. The value of ICP measured that way, is illustrated by the success to find the relationship between ICP and brain compression.
Another area where the blood flow driven decrease in venous volume can elucidate underlying function is the clinical phenomenon of ICP plateau-waves, with ICP alternating between an increased base level and systolic arterial pressure, with intact CBF at the lower ICP level.
The brain alternates between two states:
1) at a decreased intracranial venous volume, e.g. due to edema or hematoma, the voidable venous volume may approach zero, and a CBF increase may cause obstruction in a distal part of the thin-walled venous bed. Volume increase in the obstructed parts of the venous bed causes the obstruction to spread towards total obstruction, with arterial pressure in the venous and capillary beds, transmitted to ICP as plateau pressure,
2) at plateau ICP pressure CBF is obstructed. The blood flow driven distribution of the intra-venous volume, with lower volume in the flow direction is not upheld. With gradual redistribution of the blood volume in the venous bed with increasing volume in the distal parts, blood flow is gradually restored. The flow restoration decreases the intra-venous and capillary pressures, and returns ICP towards the previous, lower level.
In conclusion, the formula for the relationship between brain compression, ΔVic , and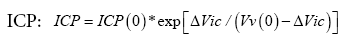 
may become a helpful tool for measurement the relation between ICP and brain volume changes, since the measurements needed are identical to those for the previous mono-exponential, elastic brain tissue, theory [3]. Since ΔVic may represent arterial volume entering intracranially at each pulse stroke, this equation also enables CBF calculation after ICP measurements.
Helpful advice from Doctor Peter Reinstrup, Department of Anesthesiology, and support from Department Clinical Neurophysiology, Skane University Hospital in Lund, is gratefully acknowledged.
