Over the last two centuries the world has changed from an industrial world to a service-oriented commercial world. Thus, the main concern of economics and efficiency researchers shifted toward service providers, such as healthcare organizations and financial institutions [1]. During the last few decades, healthcare services have become one of the fastest growing service sectors in the global economy, due to increased growth in healthcare systems costs, especially in the US [2].

Healthcare services, particularly hospitals, are naturally extremely resource intensive; so increasing their efficiency potentially yields more savings. However, unlike other types of service organizations, the considerations taken into account by decision makers in hospitals have traditionally been influenced more by clinical and medical considerations rather than by quality issues [3]. Unfortunately, some of these considerations were “a simple medical error” [4] related to some of the decisions that had been taken; they could have been revised if hospital directors had been aware of better practices [5]. Such events triggered the need for promoting access to “high-quality care that is effective, efficient, safe, timely, patient-centered, and equitable” [6].

The call for operations research studies in the healthcare sector had already been raised about 50 years ago [7]. Subsequently, many healthcare organizations are frequently evaluated in order to streamline and increase control over processes, outcomes and efficiency, [8] and numerous studies have been conducted [9]. Most studies considered only operational attributes; the minority of studies that did include clinical quality attributes [10,11] did not refer to service quality, obtained via patient satisfaction surveys [12-14]. Quality in healthcare services is a multidimensional concept; not easily defined and even more difficult to quantify [15]. The main difficulty usually lies in the perception that healthcare organizations have actually two forms of quality: Clinical (technical) quality, focusing on the “what”, and service (functional) quality that focuses on the “how” [16,17].

These calls for research and subsequent action, triggered many studies over the years, resulting in many published papers on healthcare organizations efficiency [18]. Some of them advocated “a better performance measure of hospitals that would include both quality of care and efficiency of the process” [19]. Others used a mixture of quality attributes and operations research techniques for efficiency measurement [20]; evaluated healthcare efficiency measures [21]; or checked actual outcomes of governmental reforms in healthcare [22].

The call for research also motivated the development and operation of dozens of survey systems that could measure patient or care-giver experience [23]. The most comprehensive Patient Experience Survey in US healthcare markets, was established over a decade ago [24] and is conducted quarterly by the Hospital Consumer Assessment of Healthcare Providers and Systems (HCAHPS). Its results have been used in several studies relating to patient experience. For example, Jha et al. [25] examined the relationship between several hospitals&rSQuo; key attributes, e.g., for-profit/not-for-profit, academic status and patient experience. Similarly, Isaac et al. [26] tested the relationship between clinical performance and hospitals&rSQuo; environmental characteristics, such as profit status, teaching affiliation and patient satisfaction.

However, “the effectiveness of patient experience as a performance measure is not well researched” [23]. Until recently, we have not found any published paper studying the relationships between a hospital&rSQuo;s operational efficiency and its service quality (SQ) measures. Thus, our research focuses on linking hospitals&rSQuo; SQ measures with their operational attributes outcomes; suggesting an alternative efficiency measurement model. Furthermore, SQ in healthcare services currently stands at the forefront of professional managerial attention, as it is perceived as a means of achieving better health, increasing patient satisfaction, reducing costs and gaining a better competitive advantage [27].

Analytical methods

Our study utilized a two-stage efficiency measurement procedure; the first stage involving estimation of efficiency scores, and the second stage explaining efficiency variations. The advantages of using a twostage procedure to guide public policy-makers and to assist in managerial decision-making, have already been discussed more than two decades ago [28] and have subsequently been employed in many studies [29].

For efficiency measurements, during the first stage, we used data envelopment analysis (DEA) [30]. DEA is a non-parametric, mathematical programming approach that compares the inputs and outputs of a set of homogenous decision making units, hospitals in our case, by evaluating their relative efficiency [31]. It is the most common method for hospital efficiency measurements [32]. We ran the DEA, taking into account Golany and Roll&rSQuo;s suggested workflow [33] and the proposed assumptions of Fried et al. [34].

The second stage included multivariate, Ordinary Least SQuares (OLS) regression models [35], using efficiency scores obtained in the DEA stage as a dependent variable and several SQ attributes and environmental variables as exploratory variables.

Data sources

The study utilized three public sources-the American Hospital Association (AHA) database for operational variables; the Hospital Consumer Assessment of Healthcare Providers and Systems (HCAHPS) patient satisfaction survey results for service quality attributes; and the Centers for Medicare and Medicaid Services (CMS) website for all other variables.

Based on the median value of the number of hospitals in survey papers, which is 55 [36], we searched the AHA database for a suitable US state as the target dataset. Ultimately, due to data availability and accuracy, the study consisted of 51 general acute-care hospitals in the state of New Jersey, all of which are owned by non-profit organizations and are all considered urban.

For each of the targeted hospitals, in considering the common types and number of variables for efficiency measurement, e.g., [37], eight attributes were selected and extracted from the AHA database. Six operational attributes represented the hospitals magnitude for the DEA stage; two organizational attributes represented the existence of an obstetrics service and the hospital&rSQuo;s teaching status, for the second stage. From the CMS website, we downloaded these hospitals&rSQuo; HCAHPS patient satisfaction survey results, including more than 15,000 aggregate responses, their case-mix and average length-of-stay figures.

Data preparation

Research variables were categorized into three groups: Operational variables, SQ attributes and environmental variables. The operational variables group included: (1) Total number of beds (BDS); (2) Total amount of personnel in terms of full-time-equivalent (FTE); (3) Hospital&rSQuo;s total expenses (T-EXP); (4) Total number of admissions (ADM); (5) Total number of outpatient visits (OPV); and (6) Total number of births (BRS)-only for hospitals with an OBStetrics service. To correctly take into account medical complexity, the variable ADM was replaced by a new variable named A-ADM (adjusted total admissions), calculated as a product of ADM and case-mix, as suggested by Ozcan [29].

The HCAHPS survey includes 22 service-related, multiple-choice questions [24]; its results are published as 10 aggregated experimental quality (EQ) attributes, grouped into three SQ topics: Composite, Individual and Global (Table 1). In order to determine the second stage SQ attributes, we adopted the principles of net promoter score (NPS) [38], as proposed by York and McCarthy [39], who questioned the pros and cons of using NPS, as a better measure for quality of service in healthcare. Then, using NPS principles, all EQ measures were translated into SQ ratings by subtracting “detractors” from “advocates”.

Table 1: HCAHPS experimental quality (EQ) attributes by topics.

Finally, to avoid possible redundancy, three new SQ variables, representing the three SQ topics were generated. We ran a principal component analysis on the first two SQ topics (Composite & Individual) to reduce and align their dimensionality, resulting in the creation of two new SQ components, named SQC1 and SQC2; we also chose EQ10 (henceforth, SQI) to represent the third topic (Global), as its correlation with EQ9 was nearly one (r=0.97).

Data analysis

Analyses of the 51-hospital input values shows that the average hospital utilized 328 beds (BDS); ranging from small hospitals having about 100 beds to very large hospitals, with about 700 beds. In terms of personnel, the average FTE is about 2,000 employees, ranging from 600 to over 7,000 employees. In terms of budget, their total expenses range from 100 million to almost 1.4 billion USD, with the median of about 250 million USD.

Regarding output volumes, average adjusted admissions (A-ADM) is about 27,000 patients, ranging from 7,000 patients in the smallest hospital, to almost 20 times as many in the largest hospital. The number of outpatient visits (OPV) is of a larger magnitude than admissions (ADM), varying from about 50,000 to almost three million per year. Distribution of teaching hospitals - 29 (57 percent) - versus nonteaching hospitals - 22 (43 percent) - indicates also that teaching hospitals are significantly (p value <0.01) larger, employ more inputs and produce more outputs, on average, than their non-teaching counterparts. Forty-five (45) of them (88 percent) have an OBStetrics service and their average number of births was about 2,000, whereas the rest are small hospitals, having less than 200 beds, and their total expenses (T-EXP) and personnel (FTE) are in the lowest quartile of the studied hospitals (Table 2).

Table 2: Descriptive statistics for both teaching and non-teaching hospitals (n=51).
This table summarizes the major descriptive statistics of the research variables, taking into account the hospital's teaching status.

The analysis of SQ attributes shows that the average SQI is about 0.60, ranging from the highest rating of 0.81 to the lowest rating of 0.25, while the averages of the other two SQ components, SQC1 and SQC2, are lower, about 0.55 and 0.44 respectively; ranging from the intermediate ratings of 0.65 and 0.55 to the lowest rating of 0.3 and 0.25. Additional tests show that attributes SQC2 & SQI are significantly (p value <0.001) higher amongst teaching hospitals than in nonteaching hospitals, on average, while the difference in SQC1 ratings is insignificant.

Based on recommendations by Golany and Roll [33], we omitted the variable T-EXP from the DEA model, as it showed high correlation with the two other input variables BDS & FTE, (r=0.89 and 0.96, respectively). Ultimately, the research model consisted of 13 variables (Table 3).

Table 3: Final research variables and stages.
This table summarizes the final research variables, according to its stages:

Stage I: The DEA model

The average technical efficiency (ATE) of the 51 hospitals is 0.35; 50 of them (98 percent) were considered inefficient hospitals. Additional analysis using their academic status, reveals that the Mean (ATE) and variance (ANOVA) tests were statistically significant (p value <0.05 and p value <0.001, respectively), meaning that there is a significant statistical difference between teaching and the non-teaching hospitals&rSQuo; efficiency frontier.

Stage II: Regression models

The first regression model is the following multivariate OLS model:

TE = β₀ +β₁ ·SQC₁ + β₂ ·SQC₂ + β₃ ·SQI + β₄ ·ALoS + β₅ ·T-EXP + β₆ ·OBS + β₇ ·TEA (1)

This model was established to define the relationship between the hospitals&rSQuo; efficiency scores, as an independent variable, and the exploratory variables -SQx variables, average length of stay (ALoS) and T-EXP, as dependent variables. As the outcomes of Model (1) were statistically insignificant (p value >0.2), three additional OLS regression models, using stepwise mode, were run: A multivariate model, an interaction model, and a log-based model, as a control model (Table 4).

The stepwise regression yielded only one significant (p value <0.05) variable correlated with the TE score – SQI, which implies that the two SQ components: SQC1 and SQC2, the two environmental variables: ALoS, T-EXP, and the two categorical variables: OBS and TEA, did not contribute significantly towards the explanation of the variance of TE. Thus the “best” exploratory model consists of SQI alone:

The results of Model (2) show that although the model itself was significant (p value <0.05) its R² value was quite low (R²=0.12). Therefore, we used the following log-based control model, to evaluate Model (2) robustness:

As the control model was marginally significant (at p value =0.1), we searched for a better exploratory model. Based on Anderson, Fornell and Rust [40], the following interaction OLS model, using the teaching status, was introduced:

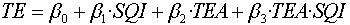
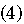
Analysis of the results of the interaction OLS regression Model (4) shows that the model and its variables are both statistically significant (p value <0.01). To support these significant outcomes, we tested the robustness of Model (4) using the following log-based control model:

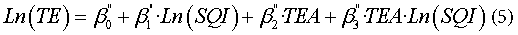
Results of the control Model (5) were statistically significant (p value <0.05), as well, supporting the robustness outcome of the &lSQuo;SQIteaching affiliation interaction&rSQuo; Model 4. (Table 4)

Table 4: A summary of the five different OLS regression models outcomes.
This table summarizes the statistic parameters results of the second stage's OLS regression models run:

Predicting technical efficiency

The variable SQI was found to be the sole significant variable amongst all second stage models. These results support the findings that SQI is significantly correlated with the TE of these 51 hospitals. As there is a statistical significant relationship between hospitals&rSQuo; TE scores, the overall likelihood that a hospital will be recommended (SQI) and their academic status (TEA), we propose the interaction Model (4) as a predictor for the hospital&rSQuo;s TE, using the following equations:

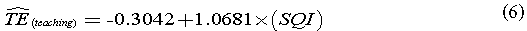
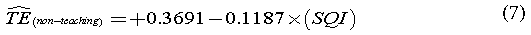
where 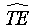equals the predicted efficiency of teaching and nonteaching hospitals, respectively.

Analyzing Eq. (6) shows that the economic elasticity (EE) of teaching hospitals is just above a unity (+1 percent), meaning that an improvement of one percentage point in a teaching hospital&rSQuo;s SQI score yields similar growth in their TE. In that case, such improvement could save an aggregate sum of more than 100 million USD per year. Simultaneously, non-teaching hospitals&rSQuo; Eq. (7) backs up the assumed trade-off between quality and efficiency [41]. Here, the motivation of improving SQI rating contradicts the need to reduce costs and to be more efficient. However, the marginal increase of a non-teaching hospital&rSQuo;s annual expenses is estimated to be 250,000 USD per one percentage point of rating.

Positioning impact matrix (PIM)

The positioning impact matrix (PIM) is a conceptual tool, used to visualize research outcomes, based on the theory of concept mapping in healthcare [42]. This plotting (Figure 1) offers a better method for handling a hospital&rSQuo;s status and relative position, before taking operational decisions, using a clusters sketch: The dashed oval cluster in the middle represents non-teaching hospitals and solid oval on the right side represents teaching hospitals.

Figure 1: Positioning Impact Matrix (PIM).

At a glance, the PIM tool shows insights that may take a considerable time to understand using common tools (e.g., pivot table). In our case, the PIM reflects some interesting facts about the hospital&rSQuo;s relative position, using four zones (Z₁):

1. The majority (83 percent) of hospitals in Z₁ are non-teaching hospitals.

2. The majority (76 percent) of teaching hospitals are in Z₂.

3. Z₃ is empty.

4. In Z₄ there are only teaching hospitals.

Additionally, using the PIM can highlight some interesting facts about the outlying hospitals, as well:

1. P₁ represents the hospital (non-teaching) with the lowest SQI value, although its inefficiency is above the median.

2. P₂ represents the hospital with the highest SQI value among the non-teaching hospitals, although it has the lowest efficiency score.

3. P₃ has the highest SQI value among the teaching hospitals, but it is far away (75 percent) from the efficiency frontier, represented by P₄, and

4. P₄ is the most efficient hospital (teaching), lying on the Paretofrontier with an efficiency score of a unity, but it has the third highest SQI value.

We believe that using the proposed PIM tool could help hospital management obtain a more focused view of their relative position and the potential impact of their decisions. For example, hospitals in Z₁ may take into account the possibility of a merger with other hospitals, preferably teaching ones.

Discussion

This study deals with one of the common debates in the healthcare world: “How can we reduce costs in the health sector, while improving the quality of care and access to services?”[43]. Until recent years, most studies measuring the performance and efficiency of hospitals have usually considered operational attributes, whereas our study addresses the association between hospitals&rSQuo; service quality and efficiency.

By studying these relationships, we try to offer a better way to make operational decisions in hospitals. Our significant statistical findings show that amongst teaching hospitals, the higher the perceived level of quality, the higher their efficiency estimate (Eq. (6)). This suggests that a better managed teaching hospital also achieves higher patient satisfaction ratings. However, amongst the non-teaching hospitals, the situation is exactly the opposite: The negative correlation implies a trade-off between service quality and efficiency (Eq. (7)).

In an attempt to find supporting explanations for our results, we analyzed several research and survey papers studying teaching hospitals. The two-stage DEA studies of Grosskopf et al. [44], questioning “whether there is a significant difference in the efficiency frontier between teaching and non-teaching hospitals?”, and Harrison et al. [45], evaluating teaching hospitals&rSQuo; clinical quality and efficiency, resulted in similar conclusions, supporting the premise that a teaching hospital can improve quality of care. Similarly, Ayanian and Weissman [46] and Kupersmith [47], who screened dozens of research papers that assessed quality of care by a hospital&rSQuo;s teaching status, concluded that teaching hospitals performed significantly better than nonteaching ones.

Although these papers did not deal directly with the relationships between service quality, efficiency and teaching status, they carried out comprehensive tests regarding similar characteristics. Therefore, we believe it possible to adopt some of their conclusions to find supporting explanations for our study results, regarding the differences between teaching and non-teaching hospitals&rSQuo; efficiency and SQ ratings, as they agreed that teaching hospitals are more efficient and have better quality of care than non-teaching ones.

This paper presents and summarizes a study that attempted to find answers to some of the meaningful questions raised, both in academia and in the healthcare world, regarding hospital efficiency and service quality; we believe that our findings contribute to this debate.

We also believe that teaching hospitals&rSQuo; managers are doing their utmost to attract patients, attain the best physicians and residents, while maintaining very high-quality standards. On the other hand, the smaller scale of non-teaching hospitals may explain some of their OBServed trade-offs between SQ ratings and operational efficiency scores.

Our research did have some limitations, such as limited access to data and decision makers. Also, as we only looked at hospitals from the State of New Jersey (for methodological purposes), this obviously limits our ability to generalize our results and conclusions. For further research, we propose several options: Using a larger sample size, including SQ attributes coupled with quantitative data, such as waiting times. A different track could be studying other types of relationship, such as the relationship between academic status and the added value for hospital services, or even developing a new model for evaluating a hospital&rSQuo;s added value.

1. Fitzsimmons JA, Fitzsimmons MJ (2006) Service management: Operations, strategy, and information technology. New-York: Irwin/McGraw-Hill Higher Education.
2. AETNA (2013) Thefactsaboutrising health carecosts.
3. Chassin MR, Galvin RW (1988) The urgent need to improve health care quality: Institute of Medicine national roundtable on health care quality. JAMA 280: 1000-1005.
4. Kohn LT, Corrigan JM, Donaldson MS (2000) To err is human: Building a Safer Health System. A report of the Committee on Quality of Health Care in America. Washington, DC: Institute of Medicine. National Academies Press.
5. Berwic DM (2002) A user’s manual for the IOM’s "Quality Chasm" report. Health Affairs 21: 80-90.
6. Institute of Medicine (2004) Insuring America’s health: Principles and recommendations. AcadEmerg Med 11: 418-422.
7. Feldstein M (1963) Operational research and efficiency in the health service. The Lancet 281: 491-493.
8. Hussey PS, DeVH, Romley J, Wang MC, Chen SS, et al. (2009) Systematic review of health care efficiency measures. Health Serv Res 44: 784-805.
9. Ouellette P, Petit P (2010) Efficiencebudgétaire des institutions de santé: Unebibliographiecommentée. Montréal: HEC Centre sur la productivitéet la prospérité. 
10. Jha AK, Li Z, Orav EJ, Epstein AM (2005) Care in US Hospitals: The Hospital Quality Alliance Program. N Engl J Med 353: 265-274.
11. Lee DS, Tu JV, Chong A, Alter DA (2008) Patient satisfaction and its relationship with quality and outcomes of care after acute myocardial infarction. Circulation 118: 1938-1945.
12. European Commission (2013) Public expenditure on health: Its growing importance, drivers and policy reforms to curb growth. Brussels: European Commission
13. Arah OA, Westert GP, Hurst J, Klazinga NS (2006) A conceptual framework for the OECD health care quality indicators project. Int J Qual Health Care 18: 5-13.
14. IOM (2001) Crossing the quality chasm: A new health system for the 21st century. Washington DC: IOM Committee on quality of health care in America.
15. Donabedian A, Wheeler JR, Wyszewianski L (1982) Quality, cost, and health: An integrative model. Medical Care 20: 975-992.
16. Grönroos C (1984) A service quality model and its marketing implications. Eur J Mar 18: 36-44.
17. Marley KA, Collier DA, Meyer GS (2004) The role of clinical and process quality in achieving patient satisfaction in hospitals. Decision Sciences 35: 349-369.
18. Li L, Benton WC (2003) Hospital Capacity Management Decisions: Emphasis on Cost Control and Quality Enhancement. Eur J Oper Res 146: 596-614.
19. Chen A, Hwang Y, Shao B (2005) Measurement and sources of overall and input inefficiencies: Evidences and implications in hospital services. Eur J Oper Res 161: 447-468.
20. Nayar P, Ozcan YA (2008) Data envelopment analysis comparison of hospital efficiency and quality. J Med Sys 32: 193-199.
21. McGlynn EA (2008) Identifying, Categorizing, and Evaluating Health Care Efficiency Measures. AHRQ Publication 8: 30.
22. Sherman BW, Behling C (2014) Beyond incentives: The impact of health care reform on employer population health management strategies. Population Health Management 17: 67-70.
23. De SD (2013) Measuring patient experience (Evidence Scan 18). London: The health foundation inspiring improvements.
24. Goldstein E, Farquhar M, Crofton C, Darby C, Garfinkel S (2005) Measuring hospital care from the patients' perspective: An overview of the CAHPS® hospital survey development process.Heal Serv Res 40: 1977-1995.
25. Jha AK, Orav EJ, Zheng J, Epstein AM (2008) Patients' perception of hospital care in the United States. New Engl J Med 359: 1921-1931.
26. Isaac T, Zaslavsky AM, Cleary PD, Landon BE (2010) The relationship between patients' perception of care and measures of hospital quality and safety. Heal Serv Res 45: 1024-1040.
27. Kaplan RS, Porter ME (2011) How to solve the cost crisis in health care. Harvard Business Review 89: 46-64.
28. Lovell CAK (1993) Production frontiers and productive efficiency. In: Fried H., Lovell C.A.K., Schmidt S. (3-67). The measurement of productive efficiency: techniques and applications. Oxford: University Press.
29. Ozcan YA (2014) Health care benchmarking and performance evaluation: An assessment using data envelopment analysis (DEA). New-York: Springer Science+Business Media.
30. Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision making units. Eur J Oper Res 2.
31. Banker RD, Charnes A, Cooper WW (1984) Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science 30: 1078-1092.
32. Hollingsworth B (2008) The measurement of efficiency and productivity of health care delivery. Heal Eco 17: 1107-1128.
33. Golany B, Roll Y (1989) An application procedure for DEA. Omega 17: 237-250.
34. Fried HO, Lovell CK, Schmidt SS, Yaisawarng S (2002) Accounting for environmental effects and statistical noise in data envelopment analysis. J Prod Anal 17: 157-174.
35. McDonald J (2009) Using least SQuares and tobit in second stage DEA efficiency analyses. European JOper Res 197: 792-798.
36. Hadji B, Meyer R, Melikeche S, Escalon S, Degoulet P (2014) Assessing the relationships between hospital resources and activities: A systematic review.J Med Sys 38: 1-21.
37. O’Neill L, Rauner M, Heidenberger K, Kraus M (2008) A cross-national comparison and taxonomy of DEA-based hospital efficiency studies. Soc-Eco Plan Sci 42: 158-189.
38. Reichheld F (2006) The ultimate question. Boston: Harvard Business School Press.
39. York AS, McCarthy KA (2011) Patient, staff and physician satisfaction: A new model, instrument and their implications. Int J HealCare Quality Assurance 24: 178-191.
40. Anderson EW, Fornell C, Rust RT (1997) Customer satisfaction, productivity, and profitability: Differences between goods and services. Marketing Science 16: 129-145.
41. Venkataraman S (2015) Cost-Quality trade-off in healthcare: Does it affect patient experience.J Qua Manag J 22: 38-45.
42. Trochim W, Kane M (2005) Concept mapping: An introduction to structured conceptualization in health care. Int J Quality Heal Care 17: 187-191.
43. HEC Montréal-Centre for Productivity and Prosperity (2012) Are our hospitals' logistics in good health.
44. Grosskopf S, Margaritis D, Valdmanis V (2004) Competitive effects on teaching hospitals. Eur J Oper Res 154: 515-525.
45. Harrison JP, Lambiase LR, Zhao M (2010)  Organizational factors associated with quality of care in US teaching hospitals.J Heal Care Fin 36: 1-12.
46. Ayanian JZ, Weissman JS (2002) Teaching hospitals and quality of care: A review of the literature. Milbank Quarterly 80: 569-593.
47. Kupersmith J (2005) Quality of care in teaching hospitals: A literature review. Academic Medicine 80: 458-466.